A review of multimodal tokenization approaches using vector quantization^[1] approaches.

Codebook Learning with Vector Quantization

VQ-VAE (NeurIPS’17)

Vector-quantized AutoEncoder (VQ-VAE)^[2] combines the variational autoencoder (VAE) with vector quantization (VQ)^[1], using the parameterization of the posterior distribution of (discrete) latents given an observation.

It does not suffer from large variance, and avoids the ‘’posterior collapse’’ issue which has been problematic with many VAEs that have a strong decoder, often caused by latents being ignored.

VAE

VAEs encompass following parts:
(1) an encoder network parameterized by a posterior distribution $q(z|x)$ of discrete latent random variables $z$ given the input data $x$, (2) a prior distribution $p(z)$, and (3) a decoder with a distribution $p(x|z)$ over input data.

Discrete latents

VQ-VAE defines the posterior and prior distributions as categorical, and the samples drawn from these distributions index an embedding table, which are used as the decoder inputs.

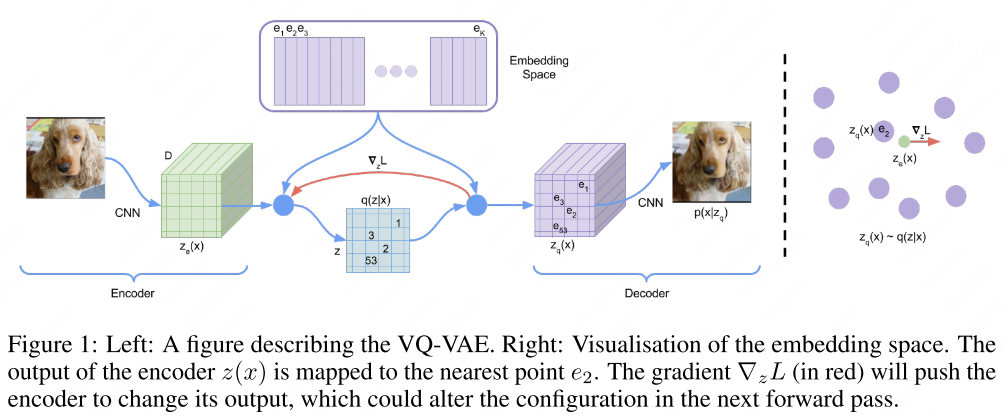
VQ-VAE defines the latent embedding space $e \in \mathbb{R}^{K \times D}$ where $K$ is the $K$-way categorical embedding table size, $D$ is the size of latent embedding vector $e_i \in \mathbb{R}^D, i \in 1,2,\cdots, K$. The encoder takes the input $x$ to get the output $z_e(x)$. The discrete latent variables $z$ are then calculated by nearest neighbour look-up using shared embedding space $e$. The posterior categorical distribution $q(z|x)$ are defined as 1-hot distribution:

$\begin{align} q(z=k|x)=\begin{cases}1&\text{for k}=\text{argmin}_j\|z_e(x)-e_j\|_2,\\0&\text{otherwise}\end{cases}, \label{eq:posterior} \end{align}$

We view this as a VAE that can bound $\log p(x)$ with the ELBO. The distribution $q(z=k|x)$ is deterministic and by defining a simple uniform prior over $z$ we obtain a KL divergence constant and equal to $\log K$.

The representation $z_e(x)$ is passed through the discretization bottleneck followed by mapping onto the nearest element of embedding $e$. The input to the decoder is the nearest embedding vector $e_k$ as follows:

$\begin{align} z_q(x)=e_k,\quad\text{where}\quad k=\text{argmin}_j\|z_e(x)-e_j\|_2 \label{eq:emb} \end{align}$

This can be treated as an autoencoder with a particular non-linearity that maps the latents to 1-of-$K$ embedding vectors.

Training

The Eq.$\eqref{eq:emb}$ and $\eqref{eq:posterior}$ approximate the gradient using straight-through estimator and just copy gradients from decoder input $z_q(x)$ to encoder output $z_e(x)$.

$\begin{align} \mathcal{L} &{}= \underbrace{\log p(x|z_q(x))}_{\text{reconstruction loss}} + \underbrace{\|\|\mathrm{sg}[z_e(x)]-e\|\|_2^2}_{\text{codebook loss}} + \underbrace{\beta\|\|z_e(x)-\mathrm{sg}[e]\|\|_2^2}_{\text{commitment loss}}, \\ &{}= \underbrace{\Vert x - D(e) \Vert_2^2}_{\text{reconstruction loss}} + \underbrace{\Vert \text{sg}[E(x)] - e \Vert_2^2}_{\text{codebook loss}} + \underbrace{\beta \Vert \text{sg}[e] - E(x) \Vert_2^2}_{\text{commitment loss}} \label{eq:vq_loss} \end{align}$

Here, $\beta=0.25$.

EMA Update

VQVAE can use exponential moving average (EMA) updates for the codebook, as the replacement for the codebook loss, the 2nd term in Eq.$\eqref{eq:vq_loss}$.

$\begin{aligned} N_{i}^{(t)} &{}:=N_{i}^{(t-1)}*\gamma+n_{i}^{(t)}(1-\gamma) \\ \quad m_{i}^{(t)} &{}:=m_{i}^{(t-1)}*\gamma+\sum_{j}^{n_{i}^{(t)}}E(x)_{i,j}^{(t)}(1-\gamma)\\ e_{i}^{(t)} &{}:=\frac{m_{i}^{(t)}}{N_{i}^{(t)}} \end{aligned}$

where $n_{i}^{(t)}$ is the number of quantized vectors in $E(x)$, $\gamma \in [0,1] $ is a decay parameter.

# reconstruction loss
loss = F.mse_loss(quantize, x.detach())
# determine code to use for commitment loss
maybe_detach = torch.detach if not self.learnable_codebook or freeze_codebook else identity

commit_quantize = maybe_detach(quantize)            

# straight through
quantize = x + (quantize - x).detach()

commit_loss = F.mse_loss(commit_quantize, x)

loss = loss + commit_loss * self.commitment_weight

VQVAE-2 (NeurIPS’19)

VQVAE-2^[3] introduces a multi-scale hierarchical structure to the original VQVAE framework, complemented by PixelCNN priors that govern the latent codes.

Stage 1: Hierarchical Latent Codes

Motivation: Hierarchical VQ models capture local features, such as textures, distinctly from global features, like the shape and geometry of objects.

VQVAE-2^[3] employs a hierarchical arrangement of VQ codes to effectively model large images. In this hierarchy, the top-level latent code encapsulates global information, while the bottom-level latent code, which is conditioned on the top-level code, is tasked with capturing local details.

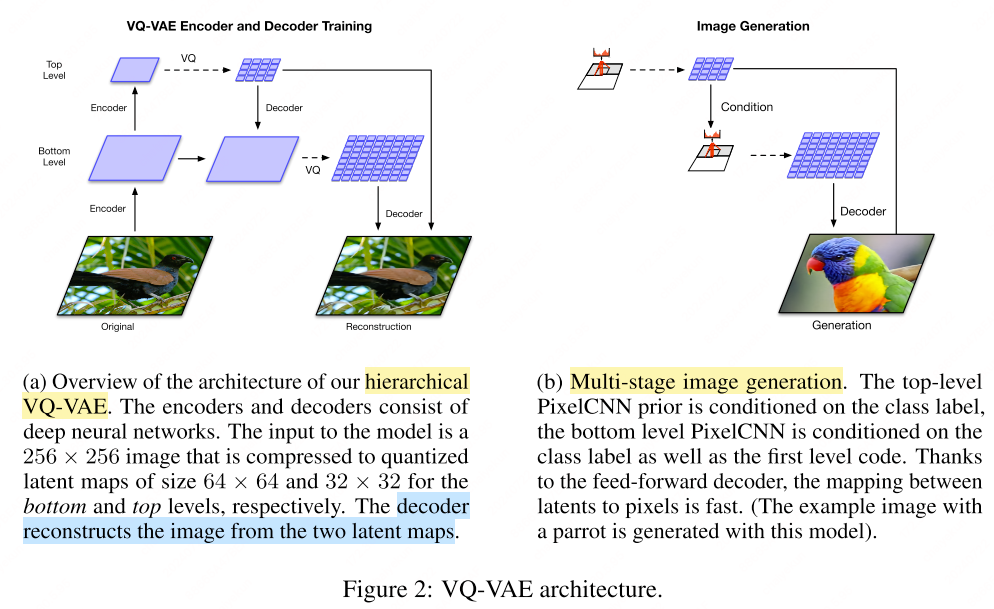
Without the conditioning of the bottom-level latent on the top-level latent, the top-level latent would be burdened with the task of encoding every minute detail from the pixels. By allowing each level in the hierarchy to focus on different aspects of the pixels, the model encourages the encoding of complementary information across each latent map. This strategy is instrumental in minimizing the reconstruction error during the encoding process. For a more in-depth understanding, refer to the algorithmic details provided.

Stage 2: Learning Priors over Latent Codes

In the second stage, VQVAE-2 learns a prior for the latent codes. It involves fitting a prior distribution to the learned posterior, effectively achieving lossless compression of the latent space. This is accomplished by re-encoding the latent variables with a distribution that more accurately approximates their true underlying distribution. Also, they find that self-attention layers can capture correlations in spatial locations that are far apart in the image.

VQGAN (CVPR’21)

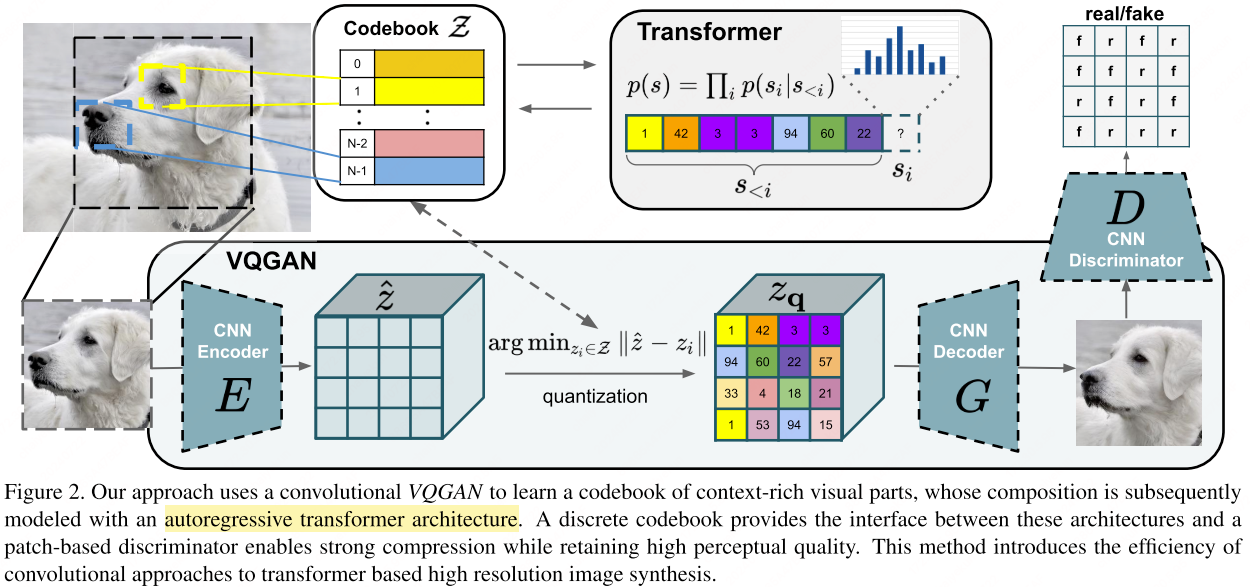
VQGAN^[4] proposes to combine CNNs with transformer architectures to learn a codebook of contextually rich visual elements. The model then utilizes the transformer’s capability to capture long-range interactions within global compositions. To ensure that the codebook effectively captures perceptually significant local structures, VQGAN employs an adversarial training strategy, reducing the transformer’s need to model low-level statistics.

QGAN employs a discriminator and perceptual loss to maintain high perceptual quality even at increased compression rates. It utilizes a patch-based discriminator, $D$, which is trained to differentiate between real and reconstructed images:

\begin{equation}
\mathcal{L}_{\mathrm{GAN}}({E,G,\mathcal{Z}},D)=[\log D(x)+\log(1-D(\hat{x}))]
\end{equation}

Here, $E$ denotes the encoder, $G$ is the generator, $\mathcal{Z} = \{z_{k}\}_{k=1}^{K} \subset \mathbb{R}^{n_{z}}$ represents the learned sicrete codebook.

The optimization objective for VQGAN is formulated as a min-max problem:

$\begin{equation} \begin{aligned}\mathcal{Q}^{*}=\arg\operatorname*{min}_{E,G,\mathcal{Z}}\operatorname*{max}_{D}\mathbb{E}_{x\sim p(x)}\Big[\mathcal{L}_{\mathrm{VQ}}(E,G,\mathcal{Z}) +\lambda\mathcal{L}_{\mathrm{GAN}}(\{E,G,\mathcal{Z}\},D)\Big]\end{aligned} \end{equation}$

The adaptive weight $\lambda$ is computed as follows:

$\begin{equation} \lambda=\frac{\nabla_{G_L}[\mathcal{L}_{\mathrm{recon}}]}{\nabla_{G_L}[\mathcal{L}_{\mathrm{GAN}}]+\delta} \end{equation}$

where $\mathcal{L}_{\mathrm{recon}}$ is the perceptual reconstruction loss, $\nabla_{G_L}[\cdot]$ denotes the gradient with respect to the last layer of the decoder.

Through this adversarial process, VQGAN not only learns to compress visual information efficiently but also ensures that the resulting images are perceptually convincing, bridging the gap between high-level semantic understanding and low-level pixel accuracy.

In the second stage, it pretrains a transformer to predict rasterized image tokens autoregressively.

iGPT (ICML’20)

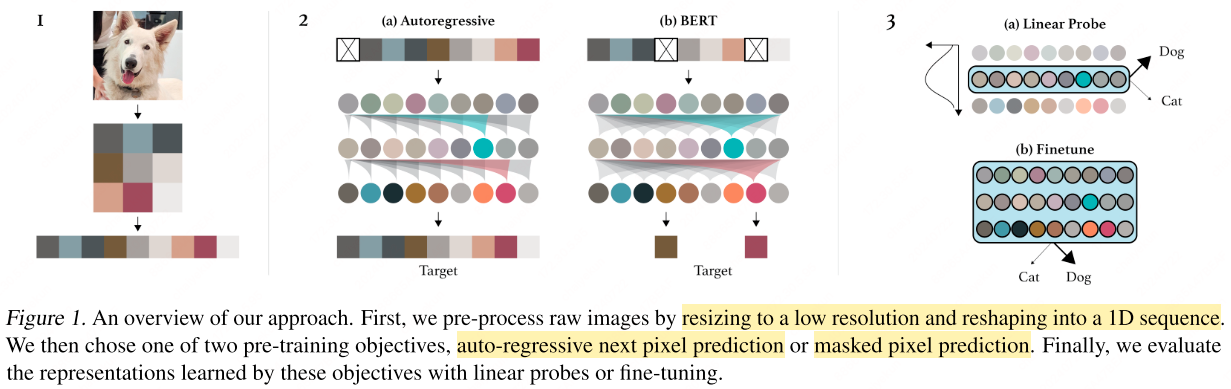
iGPT^[10] delves into the realm of autoregressive pre-training applied directly to image pixels. The process begins with reducing the image to a lower resolution to manage the extensive context that high-resolution images entail. Subsequently, iGPT employs a clustering strategy to further compress the pixel information. By applying $k$-means clustering to the (R, G, B) values of each pixel with $k$ set to 512, the model effectively condenses the color space, reducing the context length by a factor of three.

However, even after these initial steps, the resulting context—such as $96^2 \times 3$ or $192^2 \times 3$ —can remain unwieldy for efficient processing. To address this, iGPT utilizes a Variational Autoencoder with Vector Quantization (VQ-VAE) that compresses the pixel space into a latent grid of $48^2$. This transformation significantly shrinks the context size while retaining the image’s critical features.

iGPT assesses the quality of the learned representations through two different methods:

Linear Probe: This technique involves training a linear classifier on top of the frozen pre-trained representations to evaluate how well they capture the necessary information for accurate classification tasks.
Finetuning: Alternatively, the model fine-tunes the pre-trained representations on downstream tasks.

DALL-E (ICML’21)

DALL-E^[11] applies a transformer that autoregressively models the text and image tokens as a single stream of data. It uses two-stage training procedure:

Stage 1: Train a discrete VAE to compress each $256 \times 256$ RGB image into a $32 \times 32$ grid of image tokens, each element of which can assume 8192 possible values.
Stage 2: Concatenate up to 256 BPE-encoded text tokens with the $1024 (32 \times 32)$ image tokens, and train an autoregressive transformer to model the joint distribution over the text and image tokens.

The overall procedure can be viewed as maximizing the evidence lower bound (ELB) on the joint likelihood of the model distribution over iamges $x$, captions $y$, and the tokens $z$ for the encoded RGB image. We model this distribution using the factorization $p_{\theta,\psi}(x,y,z)=p_{\theta}(x\mid y,z)p_{\psi}(y,z)$ , which yields the lower bound:

$\begin{equation} \ln p_{\theta,\psi}(x,y)\geqslant\mathbb{E}_{z\sim q_{\phi}(z\mid x)}\left(\ln p_{\theta}(x\mid y,z)-\beta D_{\mathrm{KL}}(q_{\phi}(y,z\mid x),p_{\psi}(y,z))\right) \end{equation}$

where:

$q_\phi$ denotes the distribution over the $32\times 32$ image tokens generated by the dVAE encoder given the RAB image $x$;
$p_\theta$ denotes the distribution over the RGB images generated by the dVAE decoder given the image tokens;
$p_\phi$ denotes the joint distribution over the text image tokens modeled by transformer.

Stage 1: Visual Codebook Learning

DALL-E firstly train a dVAE using gumbel-softmax relaxation instead of the straight-through estimator used in VQVAE. Each $256 \times 256$ RGB image is transformed into a $32 \times 32$ grid of discrete tokens through a discrete Variational Autoencoder (dVAE). These tokens can each take on one of 8192 unique values, resulting in a compact encoding of the visual information.

The dVAE leverages a Gumbel-Softmax relaxation technique, as opposed to the straight-through estimator often used in VQ-VAE. Its architecture comprises convolutional ResNets with bottleneck-style blocks, utilizing 3x3 convolutions and 1x1 convolutions for skip connections. Downscaling of feature maps is performed by max-pooling in the encoder, while the decoder employs nearest-neighbor upsampling for reconstruction.

Stage 2: Prior Learning

The subsequent stage is focused on modeling the relationship between text and images: The model concatenates up to 256 BPE-encoded text tokens with the 1024 image tokens from Stage 1. An autoregressive transformer is then trained to capture the joint distribution of both text and image tokens.

DALL-E normalizes the cross-entropy losses for text and image tokens by their respective totals in the data batch. The text token loss is weighted by $1/8$, and the image token loss by $7/8$, reflecting a higher emphasis on image modeling.

ViT-VQGAN (ICLR’22)

ViT-VQGAN^[5] leverages ViT-based VQGAN to encode discrete latent codes, and adopt combined objectives such as logit-laplace loss, L2 loss, adversarial loss, and perceptual loss.

^[5] uses a combination of logit-laplace loss, L2 loss, perceptual loss based on VGG net, and GAN loss with a StyleGAN discriminator:

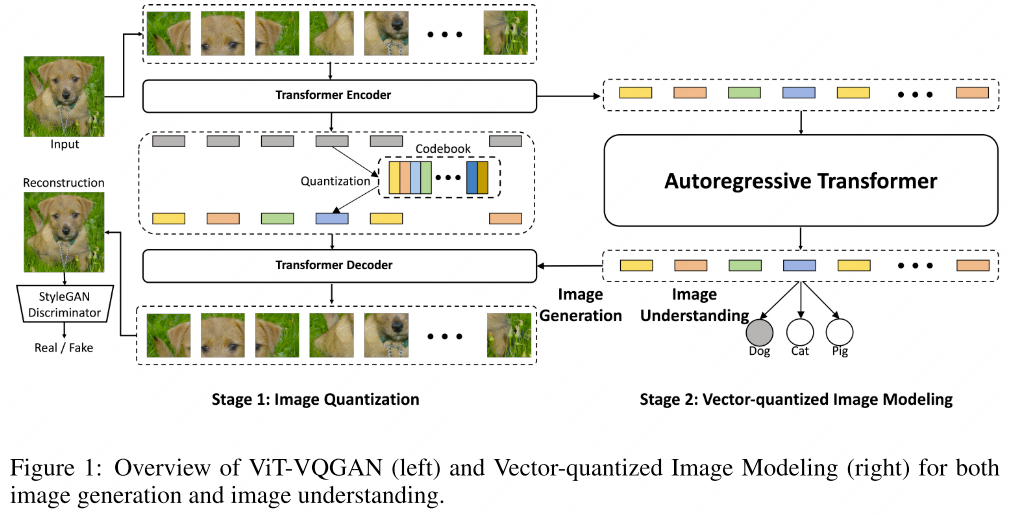
$\begin{equation} L=L_{\mathrm{VQ}}+0.1 L_{\mathrm{Adv}}+0.1 L_{\mathrm{Perceptual}}+0.1 L_{\mathrm{Logit-laplace}}+ 1.0L_{2} \end{equation}$

Dimension reduction: ^[5] finds that reducing the dimensionality of the lookup space can significantly enhance the reconstruction process. By reducing the dimensions from 256 to 32 through a linear mapping applied after the encoder’s output, the model can achieve a more efficient and accurate reconstruction of the input data.

L2-normalized codes: It applies L2 norm on encoded latents $z_e(x)$ and codebook latents $e$. The codebook variables are initialized from a normal distribution. This normalization process projects all latent variables onto the surface of a hypersphere, which means that the Euclidean distance between L2-normalized latents transitions to measuring the cosine similarity between two vectors $\|\ell_2(z_e(x))-\ell_2(e_j)\|_2^2$ . This shift to cosine similarity offers a more consistent and reliable way to compare the angles between vectors, which is particularly useful in high-dimensional spaces where Euclidean distances can become inflated and less meaningful.

RQ-VAE (CVPR’22)

The Residual-Quantized Variational Autoencoder (RQ-VAE)^[7] incorporates residual quantization (RQ) to progressively refine the quantization of a feature map in a hierarchical, coarse-to-fine approach. At each quantized position, RQ-VAE employs a sequence of $D$ residual quantization iterations, yielding $D$ discrete codes. RQ’s ability to generate a vast number of compositions—exponential in the number of iterations ($D$)—allows RQ-VAE to closely approximate feature maps without depending on an excessively large codebook. This efficiency in representation enables a reduction in the spatial resolution of the quantized feature map without compromising the integrity of the encoded image.

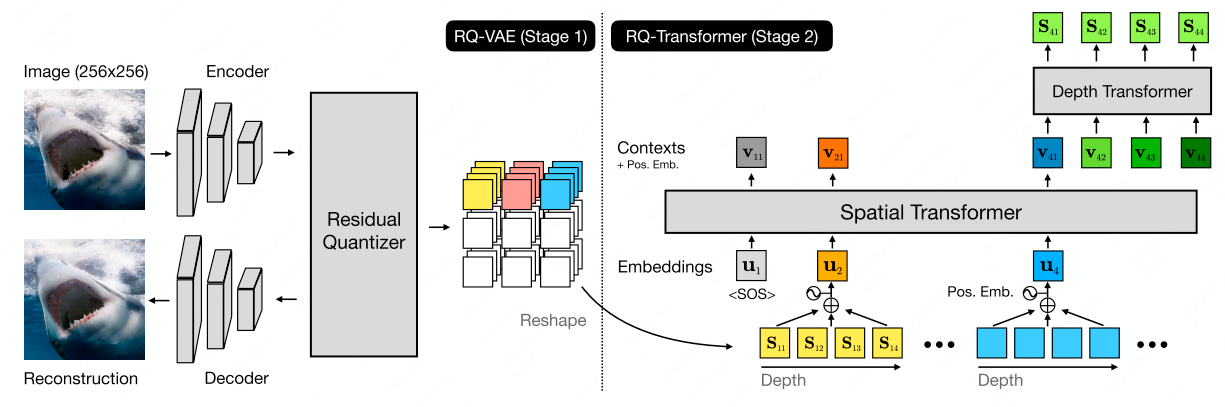
The dual-stage framework combines RQ-VAE with an RQ-Transformer, which is designed for the autoregressive modeling of images:

Stage 1: RQ-VAE encodes an image into a stacked map of $D$ discrete codes using a codebook.
Stage 2: RQ-Transformer addresses the training challenges of autoregressive models, particularly exposure bias.

Stage 1: RQ-VAE

Reducing Spatial Resolution: While VQ-VAE performs a form of lossy compression on images and necessitates a balance between dimensionality reduction and information preservation, it typically requires $HW \log_2 K$ bits to encode an image using a codebook of size $K$. According to rate-distortion theory, the minimum reconstruction error is contingent on the bit count. To reduce spatial dimensions from $(H,W)$ to $(H/2,W/2)$ while maintaining reconstruction quality, the codebook would need to increase to a size of $K^4$. However, a VQ-VAE with an expansive codebook is impractical due to the potential for codebook collapse and unstable training dynamics.

Instead of enlarging the codebook, RQ-VAE applies residual quantization to discretize a vector $z$. Given a quantization depth $D$, RQ represents $z$ with a sequence of $D$ codes:

$\begin{equation} \mathcal{RQ}(\mathbf{z};\mathcal{C},D)=(k_{1},\cdots,k_{D})\in[K]^{D} \end{equation}$

Here $\mathcal{C}$ is the codebook of size $|\mathcal{C}|=K$, and $kd$ is the code assigned to vector $z$ at depth $d$. Starting from the initial residual $r_0 = z$, RQ iteratively computes the code $k_d$ for the residual $r{d-1}$, and the subsequent residual $r_d$ is determined as follows:

$\begin{equation} k_{d}=\mathcal{Q}(\mathbf{r}_{d-1};\mathcal{C}),\\\mathbf{r}_{d}=\mathbf{r}_{d-1}-\mathbf{e}(k_{d}), \end{equation}$

This process is repeated for $d=1,\cdots, D$.

While traditional VQ segments the entire vector space $\mathbb{R}^n_z$ into $K$ distinct clusters, RQ with a depth $D$ can partition this space into $K^D$ clusters at most. This means that RQ with depth $D$ has a comparable partitioning capacity to that of a VQ with $K^D$ codes.

RQ-VAE augments the encoder-decoder structure of VQ-VAE by replacing VQ with the RQ module outlined above. With a depth of $D$, RQ-VAE represents a feature map $Z$ as a stacked map of codes $\mathbf{M}\in[K]^{H\times W\times D}$ and constructs $\hat{\mathbf{Z}}^{(d)}\in\mathbb{R}^{H\times W\times n_{z}}$ , which is quantized feature map at depth $d$ for each $d \in [D]$ such that:

$\begin{equation} \begin{aligned} \mathrm{M}_{hw} &=\mathcal{RQ}(E(\mathbf{X})_{hw};\mathcal{C},D), \\ \hat{\mathbf{Z}}_{hw}^{(d)} &=\sum_{d^{\prime}=1}^d\mathbf{e}(\mathbf{M}_{hwd^{\prime}}). \end{aligned} \end{equation}$

Finally, the decoder $G$ reconstructs the input image from $\hat{\mathbf{Z}}$ as $\hat{\mathbf{X}} = G(\hat{\mathbf{Z}})$.

The RQ-VAE training loss is as follows:

$\begin{equation} \mathcal{L}=\mathcal{L}_{\mathrm{recon}}+\beta\mathcal{L}_{\mathrm{commit}} \end{equation}$

Note that it applies the exponential moving average (EMA) of the clusted features for the codebook update.

Stage 2: RQ-Transformer

In the second stage, the RQ-Transformer employs a two-pronged approach to model images autoregressively. This stage is pivotal in enhancing the predictive accuracy of the model and can be broken down into two components:

Spatial Transformer: This module captures the contextual information by summarizing the data from preceding positions in the image. It acts like a lens, focusing on relevant areas to create a context vector that encapsulates the essence of what has been encoded so far.
Depth Transformer: Building upon the foundation laid by the Spatial Transformer, the Depth Transformer then takes a step-by-step approach to anticipate the sequence of $D$ codes for each position in the image. It does this by considering the context vector, which provides the necessary backdrop against which the predictions are made.

By combining these two transformers, the RQ-Transformer adeptly synthesizes the spatial nuances and the depth-wise details, thereby generating a comprehensive representation of the image at each step.

Contextual RQ-Transformer (NeurIPS’22)

Contextual RQ-Transformer^[9] uses two-stage framework: (1) RQVAE tokenization; (2) Contextual RQ-transformer.

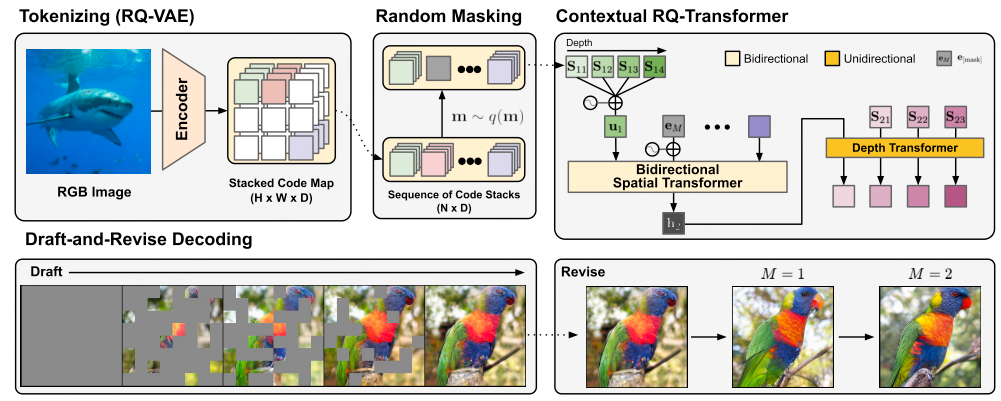
RQVAE tokenization

The first stage of the Contextual RQ-Transformer employs the RQ-VAE—a powerful tokenizer capable of condensing high-dimensional data into a discrete set of latent tokens.

Bidirectional context integration

Once the data is tokenized, the Contextual RQ-Transformer performs two key operations to model the relationships within the tokenized sequence:

Bidirectional Spatial Attention: Utilizing bidirectional attention mechanisms, the model predicts the masked positions in the sequence, given a masked scheduling function. This approach allows the model to consider both past and future context, leading to a more accurate and coherent understanding of the data.
Autoregressive Depth: The model employs autoregressive transformers to process the sequence depth-wise. This structure is akin to modifying the lower layers of a RQ-Transformer^[7] from a causal (unidirectional) to a bidirectional model. By doing so, the contextual RQ-Transformer captures the sequential dependencies with greater precision.

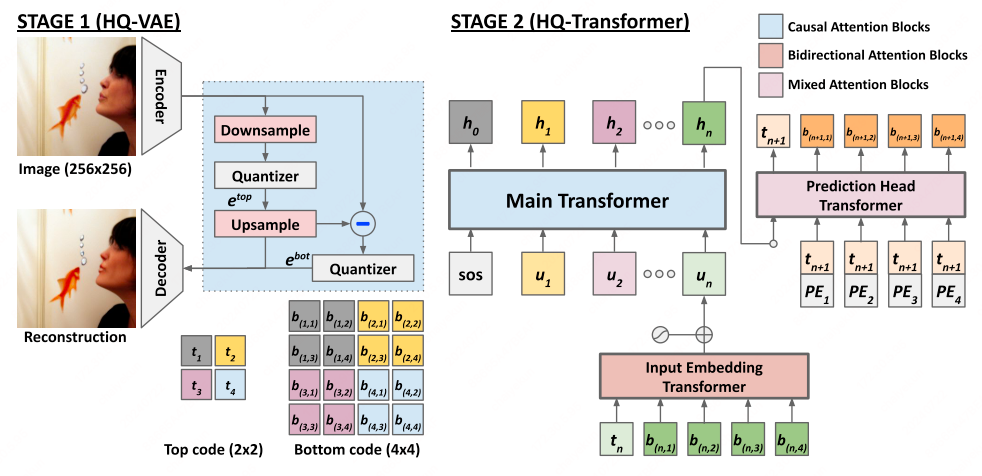
HQ-VAE (NeurIPS’22)

HQ-VAE^[12] adopts a hierarchical VQ scheme to encode input data using two levels of discrete codes, top $\mathbf{t}$ and bottom $\mathbf{b}$, respectively. It transforms the feature map $\mathbf{z} \in \mathbb{R}^{rl \times rl \times d}$ into two code maps $(\mathbf{t}, \mathbf{b})$, where $\mathbf{t} \in \mathcal{Z}^{l\times l}$ and $\mathbf{b} \in \mathcal{Z}^{rl\times rl}$ with an interger scaling factor $r \in \{1,2,\cdots \}$.

It first captures the high-level information of a feature map by quantizing its downsampled version using the top codes:

$\begin{equation} \mathbf{z}^{\mathrm{top}}=\mathrm{Downsample}(\mathbf{z};r),\quad t_{ij}=VQ^{\mathrm{top}}(\mathbf{z}_{ij}^{\mathrm{top}};\mathcal{C}_{ij}^{\mathrm{top}}),\quad\mathbf{e}_{ij}^{\mathrm{top}}=\mathcal{C}^{\mathrm{top}}[t_{ij}], \end{equation}$

where $\mathcal{C}^{\mathrm{top}}$ is the codebook of top codes. Then given the top code map $\mathbf{t}$, the bottom codes are derived at:

$\begin{equation} \mathbf{z}^{\text{bot}}=\mathbf{z}-\text{Upsample}(\mathbf{e}^{\text{top}};r),\quad b_{ij}=VQ^{\text{bot}}(\mathbf{z}^{\text{bot}};\mathcal{C}^{\text{bot}}),\quad\mathbf{e}^{\text{bot}}=\mathcal{C}^{\text{bot}}[b_{ij}], \end{equation}$

where $\mathcal{C}^{\mathrm{bot}}$ is the codebook of bottom codes.

LFQ (MagViT-V2; ICLR’24)

MagViT-V2^[8] proposed the lookup-free quantization (LFQ) method that assumes independent codebook dimensins and binary latents. Specifically, the latent space of LFQ is decomposed as Cartesian product of single-dimensional variables, as $\mathbb{C}=\times_{i=1}^{\mathrm{log}_{2}^{*}K}C_{i}$ . Given a feature vector $\mathbf{z} \in \mathbb{R}^{\log_2 K}$, each dimension of the quantized representation $q(\mathbf{z})$ is obtained from:

$\begin{equation} q(\mathrm{z}_i)=C_{i,j},\text{where}j=\arg\min_k\|\mathrm{z}_i-C_{i,k}\|, \end{equation}$

where $C_{i,j}$ is the $j$-th value in $C_i$. With $C_i = \{-1,1\}$, the $\arg\min$ can be computed by the sign function as:

$\begin{equation} q(\mathbf{z}_i)=\mathrm{sign}(\mathbf{z}_i)=-\mathbb{1}\{\mathbf{z}_i\leqslant0\}+\mathbb{1}\{\mathbf{z}_i>0\}. \end{equation}$

With LFQ, the token index for $q(\mathbf{z})$ is given by:

$\begin{equation} \text{Index}(\mathbf{z})=\sum_{i=1}^{\log_{2}K}\operatorname{arg}\operatorname*{min}_{k}\|\mathbf{z}_{i}-C_{i,k}\|\prod_{b=0}^{i-1}|C_{b}|=\sum_{i=1}^{\operatorname{log}_{2}K}2^{i-1}\mathbb{1}\{\mathbf{z}_{i}>0\} \end{equation}$

where $|C_0|=1$ sets the virtual basis.

It adds an entropy penalty during training to encourage codebook utilization:

$\begin{equation} \mathcal{L}_\text{entropy}=\mathbb{E}[H(q(\mathbf{z}))]-H[\mathbb{E}(q(\mathbf{z}))]. \end{equation}$

"""
Lookup Free Quantization
Proposed in https://arxiv.org/abs/2310.05737

In the simplest setup, each dimension is quantized into {-1, 1}.
An entropy penalty is used to encourage utilization.
"""

from math import log2, ceil
from collections import namedtuple

import torch
from torch import nn, einsum
import torch.nn.functional as F
from torch.nn import Module
from torch.cuda.amp import autocast

from einops import rearrange, reduce, pack, unpack

# constants

Return = namedtuple('Return', ['quantized', 'indices', 'entropy_aux_loss'])

LossBreakdown = namedtuple('LossBreakdown', ['per_sample_entropy', 'batch_entropy', 'commitment'])

# helper functions

def exists(v):
    return v is not None

def default(*args):
    for arg in args:
        if exists(arg):
            return arg() if callable(arg) else arg
    return None

def pack_one(t, pattern):
    return pack([t], pattern)

def unpack_one(t, ps, pattern):
    return unpack(t, ps, pattern)[0]

# entropy

def log(t, eps = 1e-5):
    return t.clamp(min = eps).log()

def entropy(prob):
    return (-prob * log(prob)).sum(dim=-1)

# class

class LFQ(Module):
    def __init__(
        self,
        *,
        dim = None,
        codebook_size = None,
        entropy_loss_weight = 0.1,
        commitment_loss_weight = 0.25,
        diversity_gamma = 1.,
        straight_through_activation = nn.Identity(),
        num_codebooks = 1,
        keep_num_codebooks_dim = None,
        codebook_scale = 1.,            # for residual LFQ, codebook scaled down by 2x at each layer
        frac_per_sample_entropy = 1.    # make less than 1. to only use a random fraction of the probs for per sample entropy
    ):
        super().__init__()

        # some assert validations

        assert exists(dim) or exists(codebook_size), 'either dim or codebook_size must be specified for LFQ'
        assert not exists(codebook_size) or log2(codebook_size).is_integer(), f'your codebook size must be a power of 2 for lookup free quantization (suggested {2 ** ceil(log2(codebook_size))})'

        codebook_size = default(codebook_size, lambda: 2 ** dim)
        codebook_dim = int(log2(codebook_size))

        codebook_dims = codebook_dim * num_codebooks
        dim = default(dim, codebook_dims)

        has_projections = dim != codebook_dims
        self.project_in = nn.Linear(dim, codebook_dims) if has_projections else nn.Identity()
        self.project_out = nn.Linear(codebook_dims, dim) if has_projections else nn.Identity()
        self.has_projections = has_projections

        self.dim = dim
        self.codebook_dim = codebook_dim
        self.num_codebooks = num_codebooks

        keep_num_codebooks_dim = default(keep_num_codebooks_dim, num_codebooks > 1)
        assert not (num_codebooks > 1 and not keep_num_codebooks_dim)
        self.keep_num_codebooks_dim = keep_num_codebooks_dim

        # straight through activation

        self.activation = straight_through_activation

        # entropy aux loss related weights

        assert 0 < frac_per_sample_entropy <= 1.
        self.frac_per_sample_entropy = frac_per_sample_entropy

        self.diversity_gamma = diversity_gamma
        self.entropy_loss_weight = entropy_loss_weight

        # codebook scale

        self.codebook_scale = codebook_scale

        # commitment loss

        self.commitment_loss_weight = commitment_loss_weight

        # for no auxiliary loss, during inference

        self.register_buffer('mask', 2 ** torch.arange(codebook_dim - 1, -1, -1))
        self.register_buffer('zero', torch.tensor(0.), persistent = False)

        # codes

        all_codes = torch.arange(codebook_size)
        bits = ((all_codes[..., None].int() & self.mask) != 0).float()
        codebook = self.bits_to_codes(bits)

        self.register_buffer('codebook', codebook, persistent = False)

    def bits_to_codes(self, bits):
        return bits * self.codebook_scale * 2 - self.codebook_scale # [-1 ,1]

    @property
    def dtype(self):
        return self.codebook.dtype

    def indices_to_codes(
        self,
        indices,
        project_out = True
    ):
        is_img_or_video = indices.ndim >= (3 + int(self.keep_num_codebooks_dim))

        if not self.keep_num_codebooks_dim:
            indices = rearrange(indices, '... -> ... 1')

        # indices to codes, which are bits of either -1 or 1

        bits = ((indices[..., None].int() & self.mask) != 0).to(self.dtype)

        codes = self.bits_to_codes(bits)

        codes = rearrange(codes, '... c d -> ... (c d)')

        # whether to project codes out to original dimensions
        # if the input feature dimensions were not log2(codebook size)

        if project_out:
            codes = self.project_out(codes)

        # rearrange codes back to original shape

        if is_img_or_video:
            codes = rearrange(codes, 'b ... d -> b d ...')

        return codes

    @autocast(enabled = False)
    def forward(
        self,
        x,
        inv_temperature = 100.,
        return_loss_breakdown = False,
        mask = None,
    ):
        """
        einstein notation
        b - batch
        n - sequence (or flattened spatial dimensions)
        d - feature dimension, which is also log2(codebook size)
        c - number of codebook dim
        """

        x = x.float()

        is_img_or_video = x.ndim >= 4

        # standardize image or video into (batch, seq, dimension)

        if is_img_or_video:
            x = rearrange(x, 'b d ... -> b ... d')
            x, ps = pack_one(x, 'b * d')

        assert x.shape[-1] == self.dim, f'expected dimension of {self.dim} but received {x.shape[-1]}'

        x = self.project_in(x)

        # split out number of codebooks

        x = rearrange(x, 'b n (c d) -> b n c d', c = self.num_codebooks)

        # quantize by eq 3.

        original_input = x

        codebook_value = torch.ones_like(x) * self.codebook_scale
        quantized = torch.where(x > 0, codebook_value, -codebook_value)

        # use straight-through gradients (optionally with custom activation fn) if training

        if self.training:
            x = self.activation(x)
            x = x + (quantized - x).detach()
        else:
            x = quantized

        # calculate indices

        indices = reduce((x > 0).int() * self.mask.int(), 'b n c d -> b n c', 'sum')

        # entropy aux loss

        if self.training:
            # the same as euclidean distance up to a constant
            distance = -2 * einsum('... i d, j d -> ... i j', original_input, self.codebook)

            prob = (-distance * inv_temperature).softmax(dim = -1)

            # account for mask

            if exists(mask):
                prob = prob[mask]
            else:
                prob = rearrange(prob, 'b n ... -> (b n) ...')

            # whether to only use a fraction of probs, for reducing memory

            if self.frac_per_sample_entropy < 1.:
                num_tokens = prob.shape[0]
                num_sampled_tokens = int(num_tokens * self.frac_per_sample_entropy)
                rand_mask = torch.randn(num_tokens).argsort(dim = -1) < num_sampled_tokens
                per_sample_probs = prob[rand_mask]
            else:
                per_sample_probs = prob

            # calculate per sample entropy

            per_sample_entropy = entropy(per_sample_probs).mean()

            # distribution over all available tokens in the batch

            avg_prob = reduce(per_sample_probs, '... c d -> c d', 'mean')
            codebook_entropy = entropy(avg_prob).mean()

            # 1. entropy will be nudged to be low for each code, to encourage the network to output confident predictions
            # 2. codebook entropy will be nudged to be high, to encourage all codes to be uniformly used within the batch

            entropy_aux_loss = per_sample_entropy - self.diversity_gamma * codebook_entropy
        else:
            # if not training, just return dummy 0
            entropy_aux_loss = per_sample_entropy = codebook_entropy = self.zero

        # commit loss

        if self.training:
            commit_loss = F.mse_loss(original_input, quantized.detach(), reduction = 'none')

            if exists(mask):
                commit_loss = commit_loss[mask]

            commit_loss = commit_loss.mean()
        else:
            commit_loss = self.zero

        # merge back codebook dim

        x = rearrange(x, 'b n c d -> b n (c d)')

        # project out to feature dimension if needed

        x = self.project_out(x)

        # reconstitute image or video dimensions

        if is_img_or_video:
            x = unpack_one(x, ps, 'b * d')
            x = rearrange(x, 'b ... d -> b d ...')

            indices = unpack_one(indices, ps, 'b * c')

        # whether to remove single codebook dim

        if not self.keep_num_codebooks_dim:
            indices = rearrange(indices, '... 1 -> ...')

        # complete aux loss

        aux_loss = entropy_aux_loss * self.entropy_loss_weight + commit_loss * self.commitment_loss_weight

        ret = Return(x, indices, aux_loss)

        if not return_loss_breakdown:
            return ret

        return ret, LossBreakdown(per_sample_entropy, codebook_entropy, commit_loss)

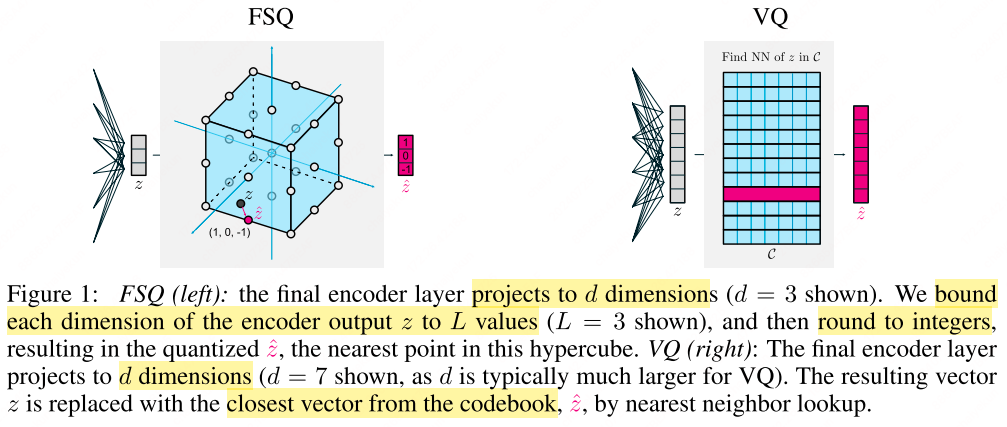
FSQ

Finite Scalar Quantization (FSQ)^[13] is a technique that applies a bounding function $f$ to a $d$-dimensional representation $z \in \mathbb{R}^d$, subsequently rounding the result to an integer. The choice of $f$ is critical, as it determines the quantization scheme. Specifically, $f$ is selected such that the output $\hat{z} = \text{round}(f(z))$ can take one of $L$ unique values. An illustrative example of $f$ is given by:

$f: z \mapsto \left\lfloor \frac{L}{2} \right\rfloor \tanh(z)$

This approach effectively maps $z$ to a quantized representation $\hat{z}$ that belongs to a codebook $\mathcal{C}$, where $\mathcal{C}$ is constructed as the product of per-channel codebook sets. Consequently, the number of distinct codebook entries is given by:

$|\mathcal{C}| = L^d$

For each vector $\hat{z} \in \mathcal{C}$, there exists a bijective mapping to an integer in the range ${1, \cdots, L^d}$, simplifying the encoding and decoding processes.

Generalized FSQ:

The concept can be further generalized to handle heterogeneous channels, where the $i$-th channel is mapped to $L_i$ unique values. This generalization yields a more flexible codebook with a total number of entries as follows:

$|\mathcal{C}| = \prod_{i=1}^d L_i$

Gradient Propagation via Straight-Through Estimator (STE):

To enable gradient propagation through the discrete round operation, we employ the Straight-Through Estimator (STE) method. This involves replacing the gradients with a simple identity term that ignores the rounding operation during backpropagation. Specifically, the STE-based rounding function is implemented as:

$\text{round_ste}: x \mapsto x + \text{sg}(\text{round}(x) - x)$

Here, sg represents the stop gradient operation, which blocks gradients from flowing through the second term, effectively treating it as a constant during backpropagation. This allows gradients to “pass through” the rounding operation, enabling training of neural networks utilizing FSQ.

def round_ste(z: Tensor) -> Tensor:
    """Round with straight through gradients."""
    zhat = z.round()
    return z + (zhat - z).detach()

"""
Finite Scalar Quantization: VQ-VAE Made Simple - https://arxiv.org/abs/2309.15505
Code adapted from Jax version in Appendix A.1
"""

from typing import List, Tuple, Optional

import torch
import torch.nn as nn
from torch.nn import Module
from torch import Tensor, int32
from torch.cuda.amp import autocast

from einops import rearrange, pack, unpack

# helper functions

def exists(v):
    return v is not None

def default(*args):
    for arg in args:
        if exists(arg):
            return arg
    return None

def pack_one(t, pattern):
    return pack([t], pattern)

def unpack_one(t, ps, pattern):
    return unpack(t, ps, pattern)[0]

# tensor helpers

def round_ste(z: Tensor) -> Tensor:
    """Round with straight through gradients."""
    zhat = z.round()
    return z + (zhat - z).detach()

# main class

class FSQ(Module):
    def __init__(
        self,
        levels: List[int],
        dim: Optional[int] = None,
        num_codebooks = 1,
        keep_num_codebooks_dim: Optional[bool] = None,
        scale: Optional[float] = None,
        allowed_dtypes: Tuple[torch.dtype, ...] = (torch.float32, torch.float64)
    ):
        super().__init__()
        _levels = torch.tensor(levels, dtype=int32)
        self.register_buffer("_levels", _levels, persistent = False)

        _basis = torch.cumprod(torch.tensor([1] + levels[:-1]), dim=0, dtype=int32)
        self.register_buffer("_basis", _basis, persistent = False)

        self.scale = scale

        codebook_dim = len(levels)
        self.codebook_dim = codebook_dim

        effective_codebook_dim = codebook_dim * num_codebooks
        self.num_codebooks = num_codebooks
        self.effective_codebook_dim = effective_codebook_dim

        keep_num_codebooks_dim = default(keep_num_codebooks_dim, num_codebooks > 1)
        assert not (num_codebooks > 1 and not keep_num_codebooks_dim)
        self.keep_num_codebooks_dim = keep_num_codebooks_dim

        self.dim = default(dim, len(_levels) * num_codebooks)

        has_projections = self.dim != effective_codebook_dim
        self.project_in = nn.Linear(self.dim, effective_codebook_dim) if has_projections else nn.Identity()
        self.project_out = nn.Linear(effective_codebook_dim, self.dim) if has_projections else nn.Identity()
        self.has_projections = has_projections

        self.codebook_size = self._levels.prod().item()

        implicit_codebook = self.indices_to_codes(torch.arange(self.codebook_size), project_out = False)
        self.register_buffer("implicit_codebook", implicit_codebook, persistent = False)

        self.allowed_dtypes = allowed_dtypes

    def bound(self, z: Tensor, eps: float = 1e-3) -> Tensor:
        """Bound `z`, an array of shape (..., d)."""
        half_l = (self._levels - 1) * (1 + eps) / 2
        offset = torch.where(self._levels % 2 == 0, 0.5, 0.0)
        shift = (offset / half_l).atanh()
        return (z + shift).tanh() * half_l - offset

    def quantize(self, z: Tensor) -> Tensor:
        """Quantizes z, returns quantized zhat, same shape as z."""
        quantized = round_ste(self.bound(z))
        half_width = self._levels // 2 # Renormalize to [-1, 1].
        return quantized / half_width
    
    def _scale_and_shift(self, zhat_normalized: Tensor) -> Tensor:
        half_width = self._levels // 2
        return (zhat_normalized * half_width) + half_width
    
    def _scale_and_shift_inverse(self, zhat: Tensor) -> Tensor:
        half_width = self._levels // 2
        return (zhat - half_width) / half_width
    
    def codes_to_indices(self, zhat: Tensor) -> Tensor:
        """Converts a `code` to an index in the codebook."""
        assert zhat.shape[-1] == self.codebook_dim
        zhat = self._scale_and_shift(zhat)
        return (zhat * self._basis).sum(dim=-1).to(int32)
    
    def indices_to_codes(
        self,
        indices: Tensor,
        project_out = True
    ) -> Tensor:
        """Inverse of `codes_to_indices`."""

        is_img_or_video = indices.ndim >= (3 + int(self.keep_num_codebooks_dim))

        indices = rearrange(indices, '... -> ... 1')
        codes_non_centered = (indices // self._basis) % self._levels
        codes = self._scale_and_shift_inverse(codes_non_centered)

        if self.keep_num_codebooks_dim:
            codes = rearrange(codes, '... c d -> ... (c d)')

        if project_out:
            codes = self.project_out(codes)

        if is_img_or_video:
            codes = rearrange(codes, 'b ... d -> b d ...')

        return codes

    @autocast(enabled = False)
    def forward(self, z: Tensor) -> Tensor:
        """
        einstein notation
        b - batch
        n - sequence (or flattened spatial dimensions)
        d - feature dimension
        c - number of codebook dim
        """

        orig_dtype = z.dtype
        is_img_or_video = z.ndim >= 4

        # standardize image or video into (batch, seq, dimension)

        if is_img_or_video:
            z = rearrange(z, 'b d ... -> b ... d')
            z, ps = pack_one(z, 'b * d')

        assert z.shape[-1] == self.dim, f'expected dimension of {self.dim} but found dimension of {z.shape[-1]}'

        z = self.project_in(z)

        z = rearrange(z, 'b n (c d) -> b n c d', c = self.num_codebooks)

        # make sure allowed dtype before quantizing

        if z.dtype not in self.allowed_dtypes:
            z = z.float()

        codes = self.quantize(z)
        indices = self.codes_to_indices(codes)

        codes = rearrange(codes, 'b n c d -> b n (c d)')

        # cast codes back to original dtype

        if codes.dtype != orig_dtype:
            codes = codes.type(orig_dtype)

        # project out

        out = self.project_out(codes)

        # reconstitute image or video dimensions

        if is_img_or_video:
            out = unpack_one(out, ps, 'b * d')
            out = rearrange(out, 'b ... d -> b d ...')

            indices = unpack_one(indices, ps, 'b * c')

        if not self.keep_num_codebooks_dim:
            indices = rearrange(indices, '... 1 -> ...')

        # return quantized output and indices

        return out, indices

Related work: Binary Spherical Quantization (BSQ)^[14].

Prior Learning

In the second stage, existing literature often applies a causal or bidirectional language models for prior learning.

Causal Transformer Modeling

It learns an autoregressive language models, such as VQGAN^[4], ViT-VQGAN^[5], DALL-E^[11], iGPT^[10], etc.

Bidirectional Transformer Modeling

Another way for image prior learning applies bidirectional modeling, such as MaskGIT^[15], MagViT-V2^[8], Muse^[16].

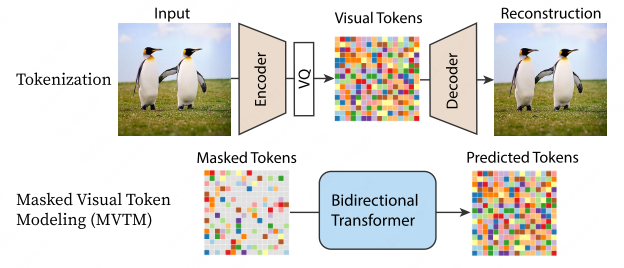
MaskGIT (CVPR’22)

MaskGIT^[15] consists of two stages:

VQ tokenizer training as in VQGAN;
Masked Visual Token Modeling (MVTM) on a bidirectional transformer.

Masked Visual Token Modeling (MVTM)

MaskGIT utilizes a mask scheduling function to strategically mask input latent tokens in bidirectional transformers. Subsequently, the masked token is refined through optimization based on the cross-entropy loss calculated between the ground-truth and predicted tokens, closely resembling the approach employed in masked language models.

Iterative Decoding

Autoregressive decoding, known for its sequential left-to-right approach, inherently leads to slower image generation. MaskGIT overcomes this limitation by incorporating bidirectional decoding, enabling parallel processing for faster results. Below is a detailed breakdown of MaskGIT’s decoding process:

Decoding Process:

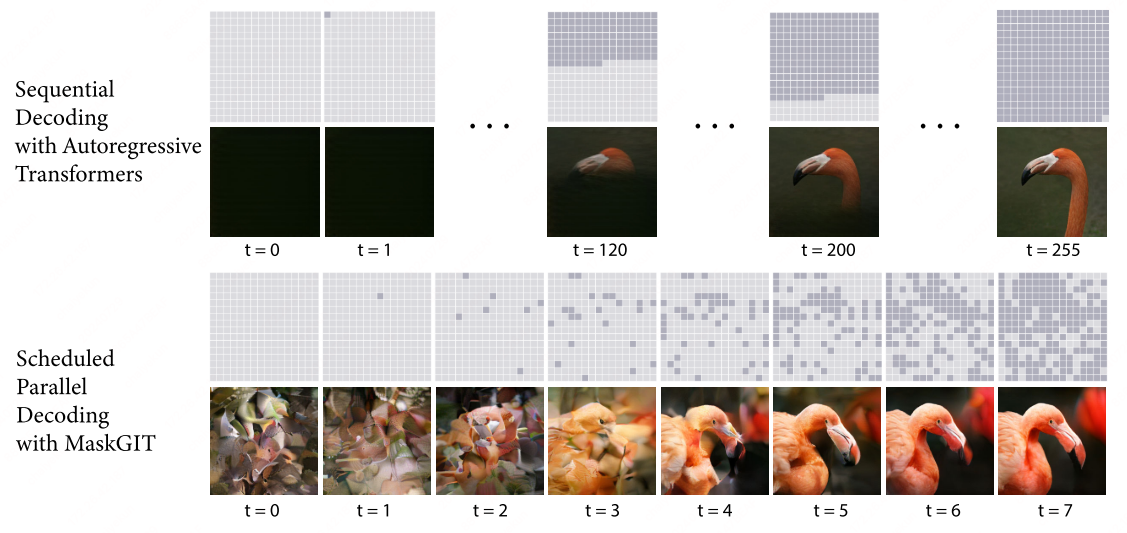
(1) Predict. At each iteration $t$, MaskGIT utilizes the current masked tokens $Y_M^{(t)}$ to predict probabilities $p^{(t)} \in \mathbb{R}^{N \times K}$ for all masked locations in parallel. This step leverages the capabilities of bidirectional transformers to simultaneously assess potential replacements for each masked token.

(2) Sample. For each masked location $i$, MaskGIT samples tokens $y_i^{(t)}$ based on the predicted probabilities $p_i^{(t)} \in \mathbb{R}^{K}$ over all possible tokens in the codebook. The sampled token’s prediction score serves as a “confidence” score, indicating the model’s certainty in its prediction. For unmasked positions in $Y_M^{(t)}$, the confidence score is set to 1.0, representing absolute certainty.

(3) Mask Schedule. The number of tokens to mask at iteration $t$ is determined using the mask scheduling function $\gamma$:

$n = \lceil\gamma\left(\frac{t}{T}\right)N\rceil$

Here, $N$ is the input length, $T$ is the total number of iterations, and $n$ is the number of tokens to be masked. As $t$ progresses, $\gamma$ ensures a decreasing mask ratio, allowing the model to gradually generate more tokens until all are uncovered within $T$ steps.

(4) Mask. To obtain $Y_M^{(t+1)}$ for iteration $t+1$, MaskGIT masks $n$ tokens in $Y_M^{(t)}$ based on their confidence scores. The mask $M^{(t+1)}$ is calculated as follows:

\begin{equation}
m_i^{(t+1)}=\begin{cases}1,&\text{if }c_i<\text{ sorted}_j(c_j)[n].\\
0,&\text{ otherwise.}\end{cases},
\end{equation}

where $c_i$ is the confidence score for the $i$-th token, and $\text{sorted}_j(c_j)[n]$ represents the $n$-th smallest confidence score among all tokens.

Synthesis in $T$ Steps: MaskGIT’s decoding algorithm systematically generates an image in $T$ iterations. At each step, the model simultaneously predicts probabilities for all masked tokens but only retains the most confident predictions. The remaining tokens are masked out and re-predicted in the next iteration. This process, with a progressively decreasing mask ratio, ensures that all tokens are generated within $T$ steps, leading to faster and more efficient image generation.

For attribution in academic contexts, please cite this work as:

@misc{chai2024VQ-Review,
  author = {Chai, Yekun},
  title = {{Multimodal Tokenization with Vector Quantization: A Review}},
  year = {2024},
  howpublished = {\url{https://cyk1337.github.io/notes/2024/05/24/Vector-Quantization/}},
}

References

1.Vector quantization (wiki) ↩
2.Van Den Oord, Aaron, and Oriol Vinyals. "Neural discrete representation learning." Advances in neural information processing systems 30 (2017). ↩
3.Razavi, Ali, Aaron Van den Oord, and Oriol Vinyals. "Generating diverse high-fidelity images with vq-vae-2." Advances in neural information processing systems 32 (2019). ↩
4.Esser, Patrick, Robin Rombach, and Bjorn Ommer. "Taming transformers for high-resolution image synthesis." Proceedings of the IEEE/CVF conference on computer vision and pattern recognition. 2021. ↩
5.Yu, Jiahui, Xin Li, Jing Yu Koh, Han Zhang, Ruoming Pang, James Qin, Alexander Ku, Yuanzhong Xu, Jason Baldridge, and Yonghui Wu. "Vector-quantized image modeling with improved vqgan." arXiv preprint arXiv:2110.04627 (2021). ↩
6.Yu, Lijun, Yong Cheng, Kihyuk Sohn, José Lezama, Han Zhang, Huiwen Chang, Alexander G. Hauptmann et al. "Magvit: Masked generative video transformer." In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pp. 10459-10469. 2023. ↩
7.Lee, D., Kim, C., Kim, S., Cho, M., & Han, W. S. (2022). Autoregressive image generation using residual quantization. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (pp. 11523-11532). ↩
8.Yu, Lijun, José Lezama, Nitesh B. Gundavarapu, Luca Versari, Kihyuk Sohn, David Minnen, Yong Cheng et al. "Language Model Beats Diffusion--Tokenizer is Key to Visual Generation." ICLR 2024. ↩
9.Lee, Doyup, et al. "Draft-and-revise: Effective image generation with contextual rq-transformer." Advances in Neural Information Processing Systems 35 (2022): 30127-30138. ↩
10.Chen, Mark, et al. "Generative pretraining from pixels." International conference on machine learning. PMLR, 2020. ↩
11.Ramesh, Aditya, et al. "Zero-shot text-to-image generation." International conference on machine learning. Pmlr, 2021. ↩
12.You, Tackgeun, et al. "Locally hierarchical auto-regressive modeling for image generation." Advances in Neural Information Processing Systems 35 (2022): 16360-16372. ↩
13.Mentzer, Fabian, et al. "Finite scalar quantization: Vq-vae made simple." arXiv preprint arXiv:2309.15505 (2023). ↩
14.Zhao, Yue, Yuanjun Xiong, and Philipp Krähenbühl. "Image and Video Tokenization with Binary Spherical Quantization." arXiv preprint arXiv:2406.07548 (2024). ↩
15.Chang, Huiwen, et al. "Maskgit: Masked generative image transformer." Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. 2022. ↩
16.Chang, Huiwen, et al. "Muse: Text-to-image generation via masked generative transformers." arXiv preprint arXiv:2301.00704 (2023). ↩