Transformer Variants: A Peek

This is an introduction of variant Transformers.^[1]

Relevant notes:

1. Transformer detailed explanation
2. Transformer variant architectures
3. BERTology introduction

Transformer

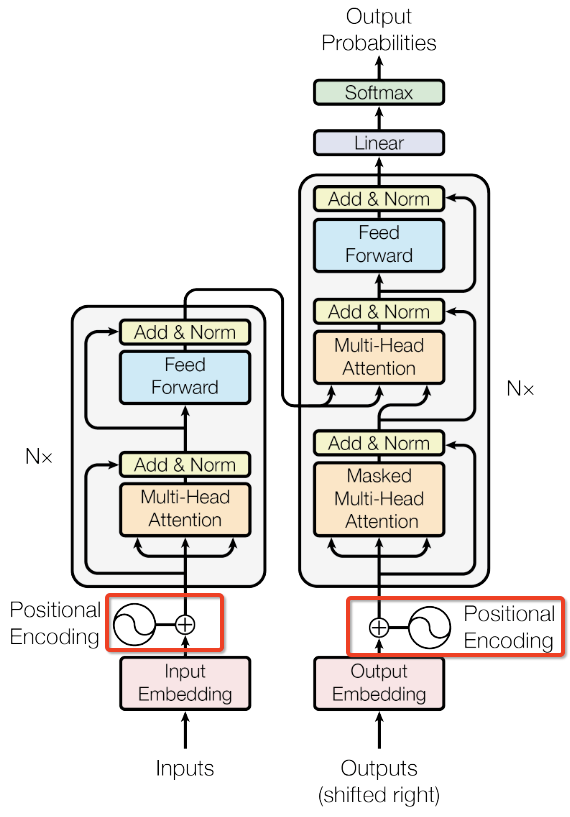
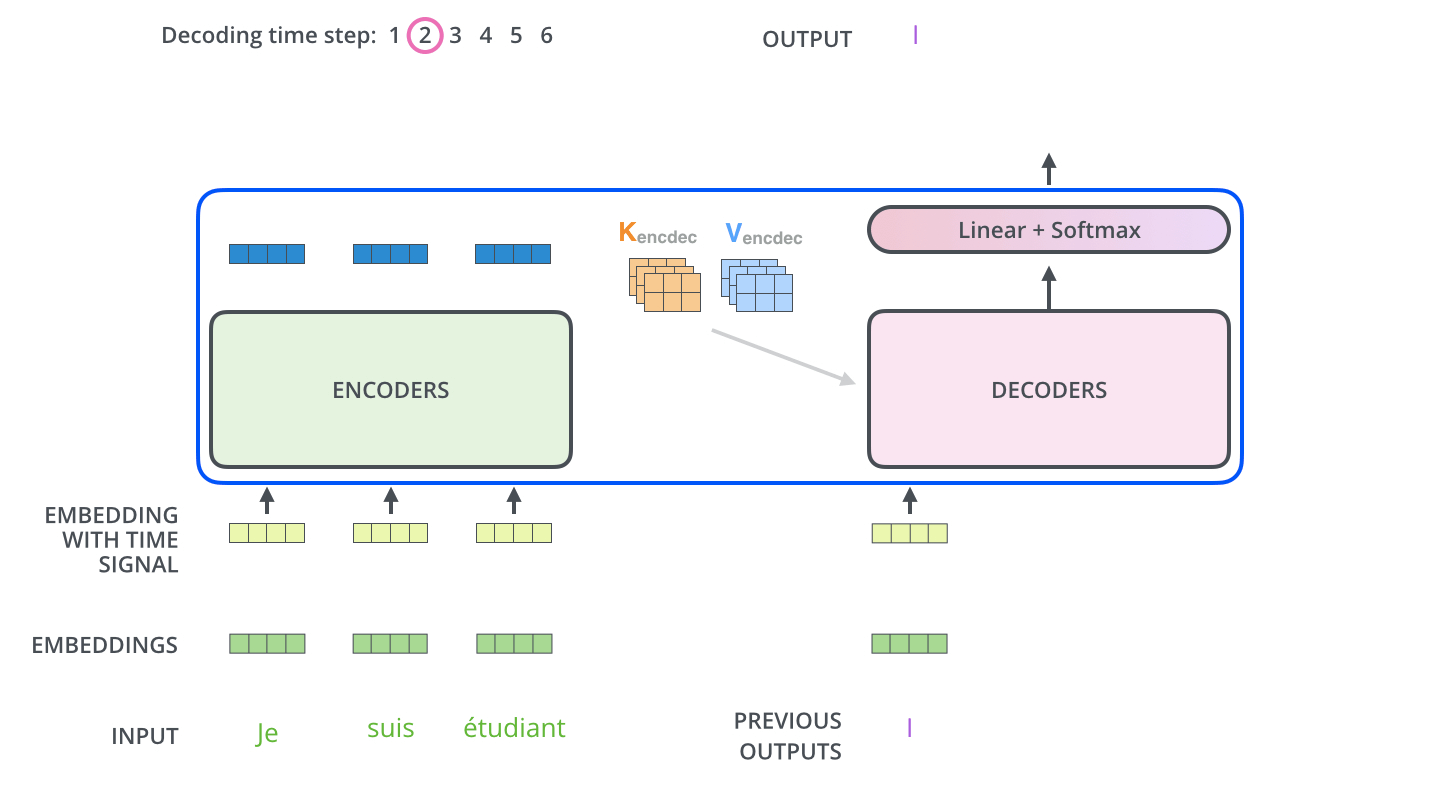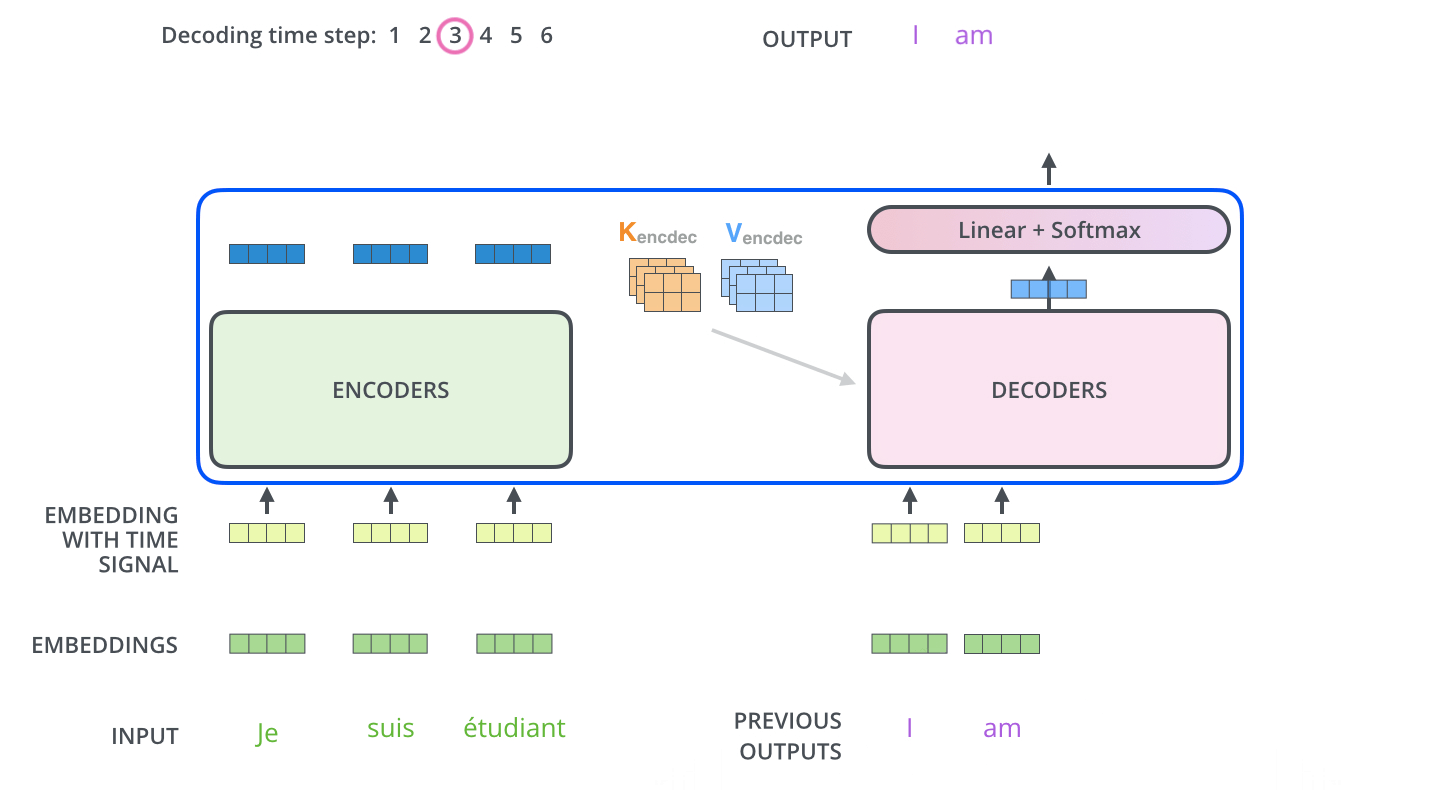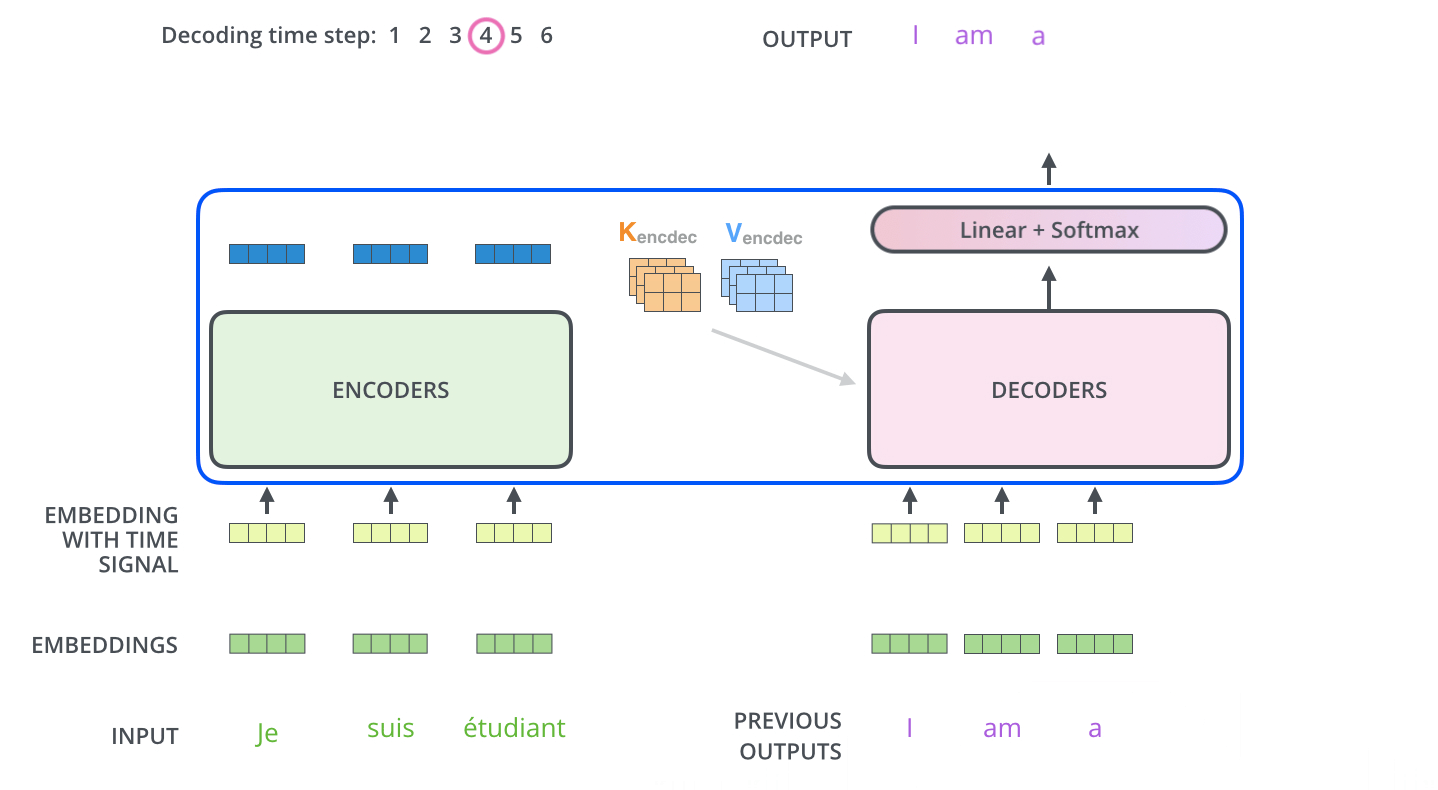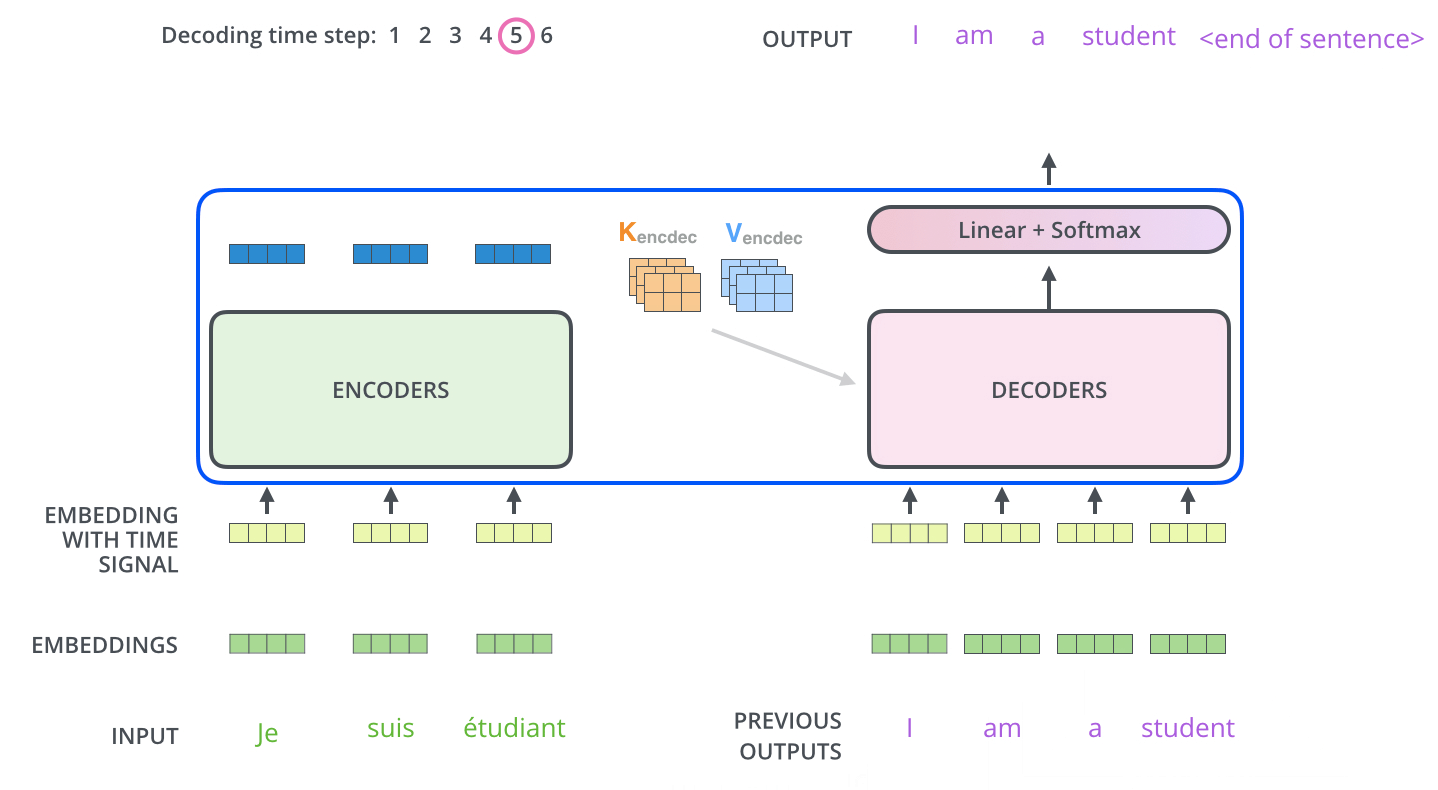
The details of transformer is explained in previous blogs. The schema of Transformer is as following fig.

• Architecture
  
• Decoding
  

Vanilla Transformer

It is impossible to preprocess the entire context sequence in the whole corpus from the beginning, due to the limited resource in practice.

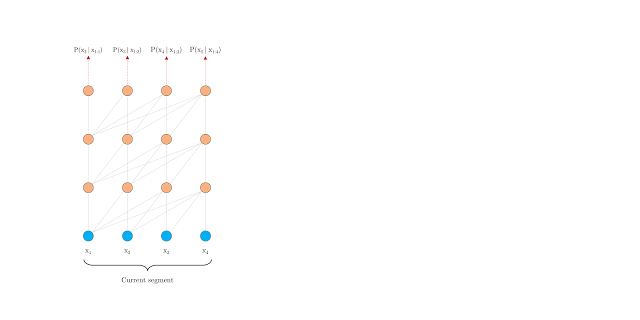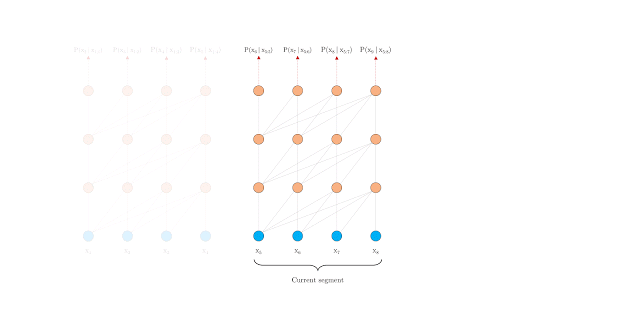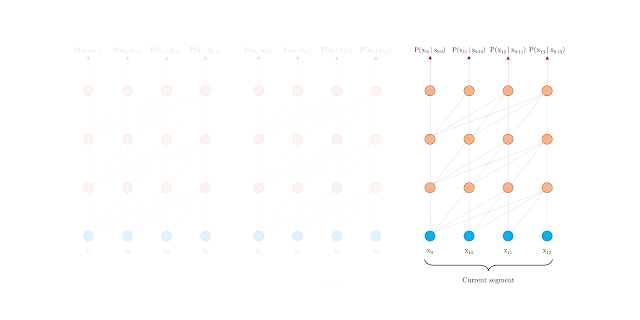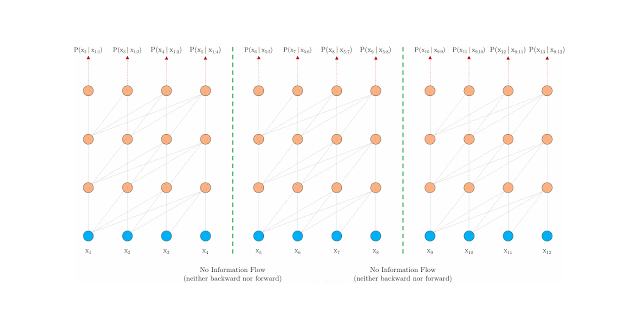
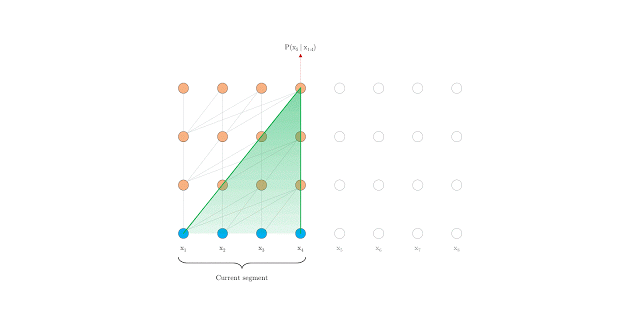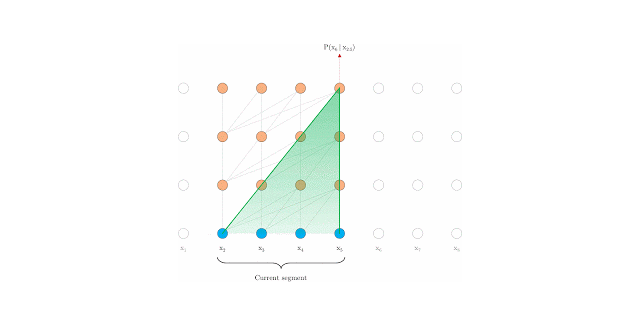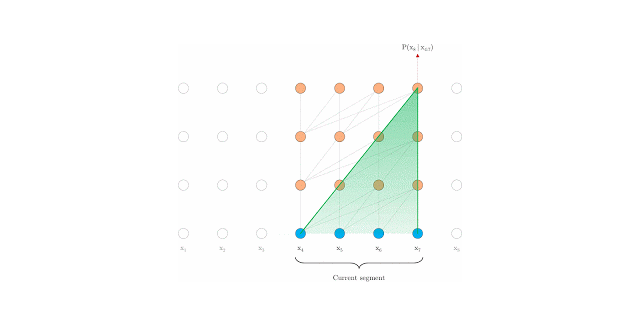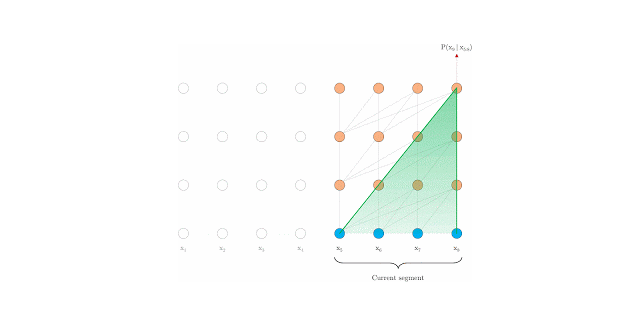
Vanilla Transformer (Al-Rfou et. al 2019)^[2] splits the entire corpus into shorter segments, and train within each segment. This leads to the context fragmentation problem by ignoreing all contextual information from previous segments.

As in above fig., information never flows across segements.

• Evaluation
  
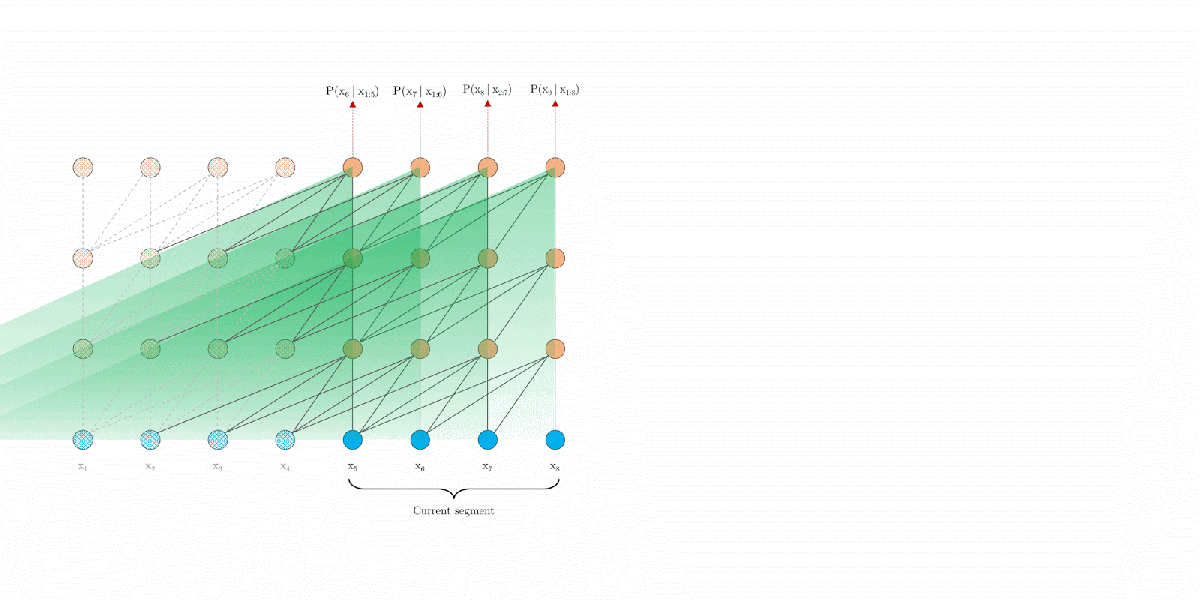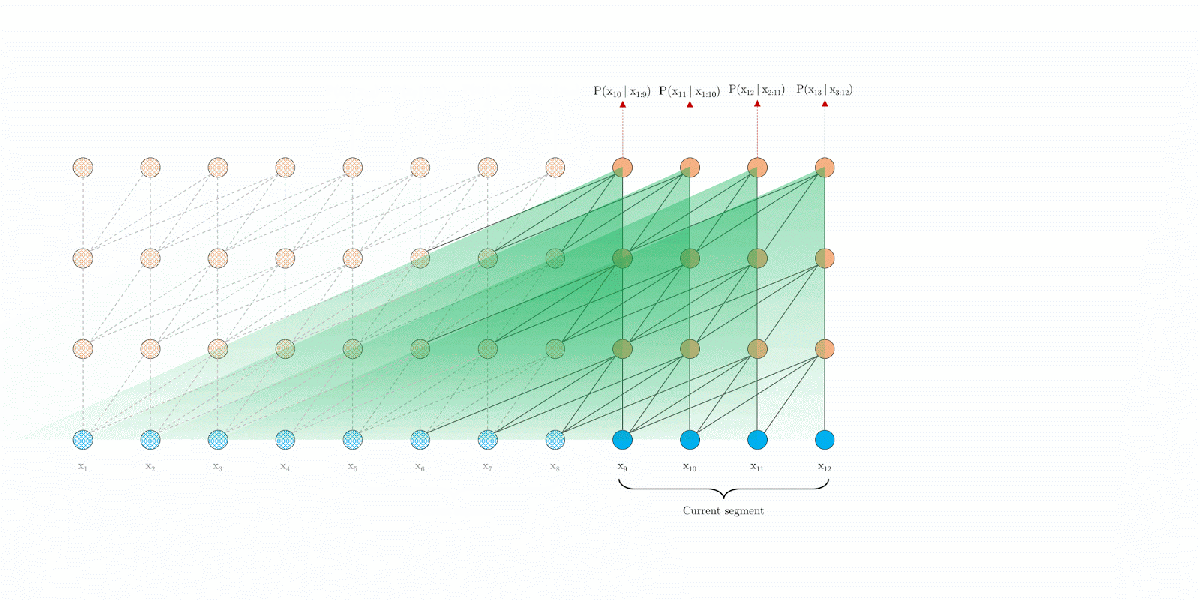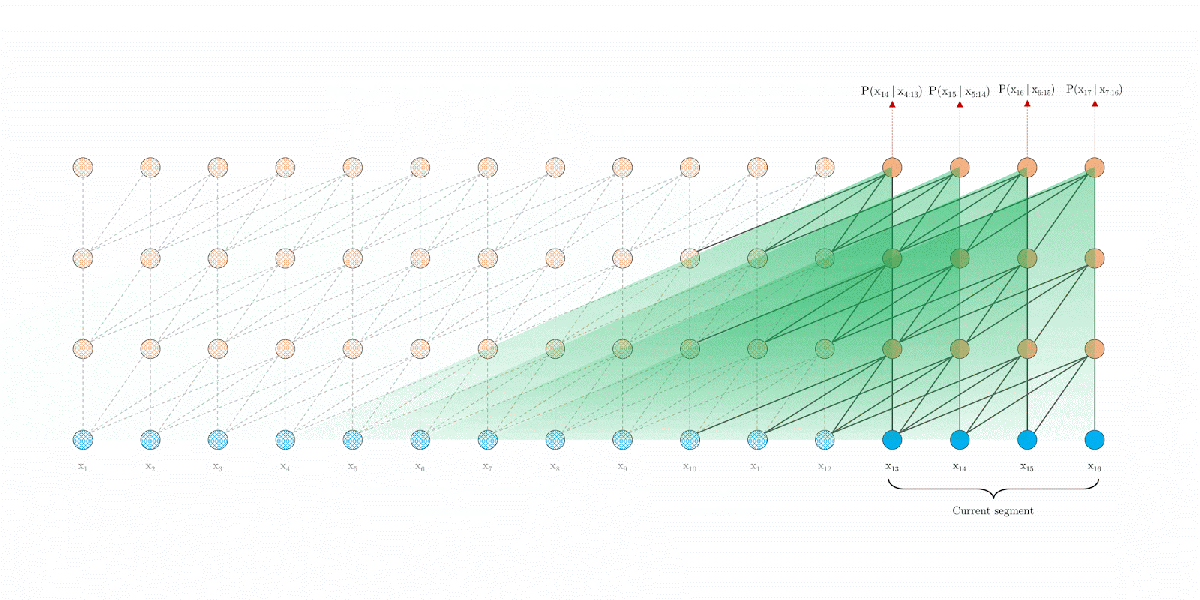
  During evaluation, for each output step, the segment shifts right by only one position, which hurts the decoding efficiency and speed.

Relative Positional Representation(RPR)

• Relation-aware self-attn
  Consider the pairwise relationships between input elements, which can be seen as a labeled, directed fully-connected graph. Let $a_{ij}^V,a_{ij}^K \in \mathbb{R}^{d_a}$ represent the edge between input elements $x_i$ and $x_j$.

Then add the pairwise information to the sublayer output:

$$\begin{align} e_{ij} &= \frac{x_i W^Q (x_j W^K \color{red}{+a_{ij}^K})^\top}{\sqrt{d_z}} \\ &= \frac{x_i W^Q (x_jW^K)^\top + \overbrace{\color{green}{\pmb{x_iW^Q(a_{ij}^K)^\top}}}^\text{efficient implementation}}{\sqrt{d_z}} \\ \alpha_{ij} &= \frac{\exp e_{ij}}{\sum_{k=1}^n \exp e_{ik}} \\ z_i &= \sum_{j=1}^n \alpha_{ij}(x_jW^V \color{red}{+ a_{ij}^V} )\\ \end{align}$$

• Clip RPR
  $k$ denotes the maximum relative position. The relative position information beyond $k$ will be clipped to the maximum value, which generalizes to the unseen sequence lengths during training.^[5] In other words, RPR only considers context in a fixed window size $2k+1$, indicating $k$ elements on the l.h.s, and $k$ elements on the r.h.s, as well as itself.

$$\begin{align} \text{clip}(x,k) &= \max(-k, \min(k,x)) \\ a_{ij}^K &= w_{\text{clip}(j-i, k)}^K \\ a_{ij}^V &= w_{\text{clip}(j-i, k)}^V \end{align}$$

where rpr $w^K = (w_{-k}^K, \cdots, w_k^K) \in \mathbb{R}^{d_a}$ and $w^V = (w_{-k}^V, \cdots, w_k^V) \in \mathbb{R}^{d_a}$ are learnable.

Trainable param number:

• MADPA: $\overbrace{4 \times \big(\text{d_model} \times \text{d_model} + \text{d_model} \big)}^\text{4 dense layers}$

• MADPA with RPR: $\underbrace{4 \times \big(\text{d_model} \times \text{d_model} + \text{d_model} \big)}_\text{4 dense layers} + \underbrace{\color{red}{2 \times (\text{seq_len}^2 \times d_k )}}_\text{2 RPR matrices}$

• My PyTorch implementation

  class MultiHeadedAttention_RPR(nn.Module):
      """ @ author: Yekun CHAI """
      def __init__(self, d_model, h, max_relative_position, dropout=.0):
          """
          multi-head attention
          :param h: nhead
          :param d_model: d_model
          :param dropout: float
          """
          super(MultiHeadedAttention_RPR, self).__init__()
          assert d_model % h == 0
          #  assume d_v always equals d_k
          self.d_k = d_model // h
          self.h = h
          self.linears = utils.clones(nn.Linear(d_model, d_model), 4)
          self.dropout = nn.Dropout(p=dropout)
  
          self.max_relative_position = max_relative_position
          self.vocab_size = max_relative_position * 2 + 1
          self.embed_K = nn.Embedding(self.vocab_size, self.d_k)
          self.embed_V = nn.Embedding(self.vocab_size, self.d_k)
  
      def forward(self, query, key, value, mask=None):
          """
          ---------------------------
          L : target sequence length
          S : source sequence length:
          N : batch size
          E : embedding dim
          ---------------------------
          :param query: (N,L,E)
          :param key: (N,S,E)
          :param value: (N,S,E)
          :param mask:
          """
          nbatches = query.size(0)  # batch size
          seq_len = query.size(1)
          # 1) split embedding dim to h heads : from d_model => h * d_k
          # dim: (nbatch, h, seq_length, d_model//h)
          query, key, value = \
              [l(x).view(nbatches, -1, self.h, self.d_k).transpose(1, 2)
               for l, x in zip(self.linears, (query, key, value))]
  
          # 2) rpr
          relation_keys = self.generate_relative_positions_embeddings(seq_len, seq_len, self.embed_K)
          relation_values = self.generate_relative_positions_embeddings(seq_len, seq_len, self.embed_V)
          logits = self._relative_attn_inner(query, key, relation_keys, True)
          weights = self.dropout(F.softmax(logits, -1))
          x = self._relative_attn_inner(weights, value, relation_values, False)
          # 3) "Concat" using a view and apply a final linear.
          # dim: (nbatch, h, d_model)
          x = x.transpose(1, 2).contiguous().view(nbatches, -1, self.h * self.d_k)
          return self.linears[-1](x)
  
      def _generate_relative_positions_matrix(self, len_q, len_k):
          """
          genetate rpr matrix
          ---------------------------
          :param len_q: seq_len
          :param len_k: seq_len
          :return: rpr matrix, dim: (len_q, len_q)
          """
          assert len_q == len_k
          range_vec_q = range_vec_k = torch.arange(len_q)
          distance_mat = range_vec_k.unsqueeze(0) - range_vec_q.unsqueeze(-1)
          disntance_mat_clipped = torch.clamp(distance_mat, -self.max_relative_position, self.max_relative_position)
          return disntance_mat_clipped + self.max_relative_position
  
      def generate_relative_positions_embeddings(self, len_q, len_k, embedding_table):
          """
          generate relative position embedding
          ----------------------
          :param len_q:
          :param len_k:
          :return: rpr embedding, dim: (len_q, len_q, d_k)
          """
          relative_position_matrix = self._generate_relative_positions_matrix(len_q, len_k)
          return embedding_table(relative_position_matrix)
  
      def _relative_attn_inner(self, x, y, z, transpose):
          """
          efficient implementation
          ------------------------
          :param x: 
          :param y: 
          :param z: 
          :param transpose: 
          :return: 
          """
          nbatches = x.size(0)
          heads = x.size(1)
          seq_len = x.size(2)
  
          # (N, h, s, s)
          xy_matmul = torch.matmul(x, y.transpose(-1, -2) if transpose else y)
          # (s, N, h, d) => (s, N*h, d)
          x_t_v = x.permute(2, 0, 1, 3).contiguous().view(seq_len, nbatches * heads, -1)
          # (s, N*h, d) @ (s, d, s) => (s, N*h, s)
          x_tz_matmul = torch.matmul(x_t_v, z.transpose(-1, -2) if transpose else z)
          # (N, h, s, s)
          x_tz_matmul_v_t = x_tz_matmul.view(seq_len, nbatches, heads, -1).permute(1, 2, 0, 3)
          return xy_matmul + x_tz_matmul_v_t

• Tensorflow implementation: ^[7]

Transformer-XL

Transformer-XL^[3] is capable of learning the long-term dependency between different context fragments in Vanilla Transformers. It mainly employs the segment-level recurrence and relative positional encoding scheme.

Segment-level recurrence

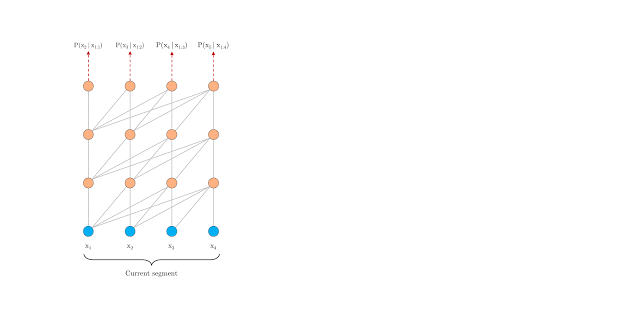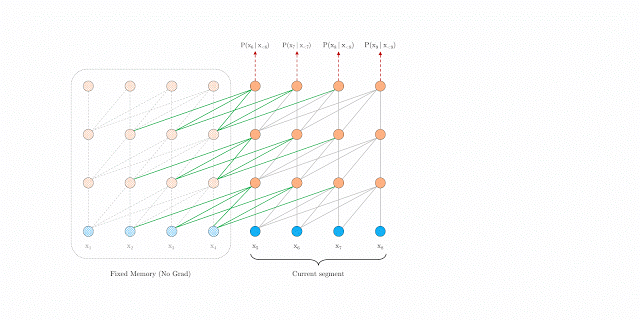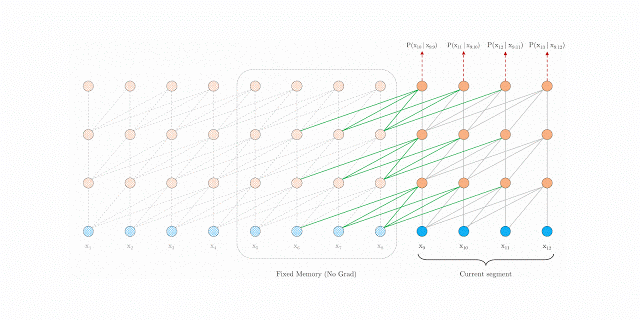
During training, transformer-xl adopts both current and the previous segments, levaraging the recurrence mechanism on segement level.

Let the consecutive segment of length $L$ be $\pmb{s}_\tau = [x_{\tau,1}, \cdots, x_{\tau,L}]$ and $\pmb{s}_{\tau+1}=[x_{\tau+1,1}, \cdots, x_{\tau+1,L}]$. Denote the $d$-dimensional hidden state of $n$-th layer for the $\tau$-th segment $\pmb{s}_\tau$, be $\pmb{h}_\tau^n \in \mathbb{R}^{L \times d}$.

$$\begin{align} \pmb{q}_{\tau+1}^{n} &= \pmb{h}_{\color{red}{\tau+1}}^{n-1} \pmb{W}_q^\top \\ \pmb{k}_{\tau+1}^{n} &= [\overbrace{\text{SG}(\pmb{h}_{\color{red}{\tau}}^{n-1})}^\text{stop gradient}; \pmb{h}_{\color{red}{\tau+1}}^{n-1})] \pmb{W}_k^\top & \text{concat hidden states of prev segments} \\ \pmb{v}_{\tau+1}^{n} &= [\underbrace{\text{SG}(\pmb{h}_{\color{red}{\tau}}^{n-1})}_\text{stop gradient}; \pmb{h}_{\color{red}{\tau+1}}^{n-1})] \pmb{W}_v^\top & \text{concat hidden states of prev segments}\\ \pmb{h}_{\tau+1}^n &= \text{Transformer}(\pmb{q}_{\tau+1}^n, \pmb{k}_{\tau+1}^n, \pmb{v}_{\tau+1}^{n}) \\ \end{align}$$

Thus, the recurrent dependency between $\pmb{h}_{\tau+1}^n$ and $\pmb{h}_{\tau}^{n-1}$ shifts one layer vertically and one segment horizontally, unlike the recurrence of same layer in RNNs. As a result, the largest long-range dependency length is linearly w.r.t # of layers times segment length, i.e. $O(N \times L)$.

• Evaluation
  During evaluation process, the representation from previous segments can be reused, which is much faster compared with vanilla Transformers (as below fig.).
  

Positional Encoding

Absolute Positional Encoding

• Problems: In the segment $\tau$, using the same absolute positional encoding $\pmb{U}_{1:L}$ for all segments cannot distinguish the positional difference between the same place in different segments, i.e. $x_{\tau,j}$ and $x_{\tau+1,j}$ for any $j=1, \cdots, L$.^[1]

$$\begin{align} \pmb{A}_{i,j}^\text{abs} &= q_i^\top k_j \\ & = \big(W_q(E+\color{red}{U})_{i,\bullet} \big)^\top \big(W_k(E+\color{orange}{U})_{\bullet,j}\big) \\ &= (E_{i,\bullet}^\top W_q^\top + \color{red}{U_{i,\bullet}^\top W_q^\top} ) (W_k E_{\bullet,j} + \color{orange}{W_k U_{\bullet,j}}) \\ &= \underbrace{E_{i,\bullet}^\top W_q^\top W_k E_{\bullet,j} }_\text{(a)} + \underbrace{E_{i,\bullet}^\top W_q^\top \color{orange}{W_k U_{\bullet,j}} }_\text{(b)} \\&+ \underbrace{\color{red}{U_{i,\bullet}^\top W_q^\top} W_k E_{\bullet,j}}_\text{(c)} + \underbrace{ \color{red}{U_{i,\bullet}^\top W_q^\top} \color{orange}{W_k U_{\bullet,j}} }_\text{(d)} \end{align}$$

Here,

• (a) captures content-based information, i.e., how much attention the word in row-$i$ pays to word in col-$j$ despite the position.
• (b) captures content-dependent positional bias, representing how much the word in row-$i$ should attend to position $j$.
• (c) defines the global content biases, denoting how much the position-$i$ should attend to words in $j$-th position.
• (d) denotes the global positional bias, i.e., the soft attention that words in position $i$ should pay to a row in position $j$.

Relative positional encoding

Solution: use relative positional encoding. Conceptionally, positional encoding (pe) gives the temporal clue or biases about how information should be gathered, i.e., where to attend.^[3] It is sufficient to know the relative distance beween each key vector $k_{\tau,j}$ and itself $k_{\tau,i}$, i.e. $i-j$.

Replacement:

1. replace all absolute pe’s $U_j$ in (b) and (d) with relative counterpart $\color{cyan}{R_{i-j}}$, which is a sinusoid encoding matrix without learnable weights.
2. replace the query $\color{red}{U_{i,\bullet}^\top W_q^\top}$ with a trainable parameter $\color{blue}{u \in \mathbb{R}^d}$ and similarly, $\color{blue}{v \in \mathbb{R}^d}$ in (d). Because the query vector is the same for all query positions, meaning that the query bias attending to words at various positions should be identical, no matter the query positions.
3. substitude the weight of key vector with two matrices $\color{Salmon}{W_{k,E}}$ and $\color{ForestGreen}{W_{k,R}}$ respectively, to produce the $\color{Salmon}{\text{content-based}}$ and $\color{Green}{\text{location-based}}$ key vectors. $$\begin{align} A_{i,j}^\text{rel} &= \underbrace{E_{i,\bullet}^\top W_q^\top \color{Salmon}{W_{k,E}} E_{\bullet,j} }_\text{(a)} + \underbrace{E_{i,\bullet}^\top W_q^\top \color{Green}{W_{k,R} } \color{cyan}{R_{i-j}} }_\text{(b)} \\&+ \underbrace{\color{blue}{u^\top} \color{Salmon}{W_{k,E}} E_{\bullet,j}}_\text{(c)} + \underbrace{ \color{blue}{v^\top} \color{Green}{W_{k,R}} \color{Cyan}{R_{i-j}} }_\text{(d)} \end{align}$$

Thus,

• (a) denotes content-based addressing
• (b) captures content-dependent positional bias
• (c) denotes the global bias
• (d) represents the global positional bias

The PyTorch implementation:

class TransformerXL(nn.Module):
    def __init__(self, d_model, n_head, d_head, mem_len, n_layer, clamp_len, tgt_len,
                 ext_len, dropatt, d_inner, pre_lnorm, dropout):
        self.n_layer = n_layer
        self.mem_len = mem_len
        self.word_emb = _
        self.clamp_len = clamp_len
        self.d_model = d_model
        self.n_head = n_head
        self.d_head = d_head
        self.drop = nn.Dropout(p=dropout)
        self.layers = nn.ModuleList()

        for i in range(n_layer):
            self.layers = self.layers.append(RelPartialLearnableDecLayer(
                n_head, d_model, d_head, d_inner, dropout, tgt_len=tgt_len,
                ext_len=ext_len, mem_len=mem_len, dropatt=dropatt, pre_lnorm=pre_lnorm))

    def _create_params(self):
        self.pos_emb = PositionEmbedding(self.d_model)
        self.r_w_bias = nn.Parameter(torch.Tensor(self.n_head, self.d_head))
        self.r_r_bias = nn.Parameter(torch.Tensor(self.n_head, self.d_head))

    def init_mems(self):
        if self.mem_len > 0:
            mems = []
            param = next(self.parameters())
            for _ in range(self.n_layer + 1):
                empty = torch.empty(0, dtype=param.dtype, device=param.device)
                mems.append(empty)
            return mems
        else:  # do not use mems
            return None

    def _update_mems(self, hids, mems, qlen, mlen):
        if mems is None: return

        assert len(hids) == len(mems), 'len(hids) != len(mems)!'

        with torch.no_grad():
            new_mems = []
            end_idx = mlen + qlen
            beggin_idx = max(0, end_idx - self.mem_len)
            for i in range(len(hids)):
                cat = torch.cat((mems[i], hids[i]), dim=0)
                new_mems.append(cat[beggin_idx:end_idx].detach())
        return new_mems

    def _forward(self, inp, mems=None):
        qlen, bsz = inp.szie()
        word_emb = self.word_emb(inp)

        mlen = mems[0].size(0) if mems is not None else 0
        klen = mlen + qlen

        dec_attn_mask = torch.triu(word_emb.new_ones(qlen, klen), diagnal=1 + mlen).byte()[:, :, None]

        hiddens = []
        pos_seq = torch.arange(klen - 1, -1, -1.0, device=word_emb.device, dtype=word_emb.dtype)
        if self.clamp_len > 0:
            pos_seq.clamp_(max=self.clamp_len)
        pos_emb = self.pos_emb(pos_seq)

        core_out = self.drop(word_emb)
        pos_emb = self.drop(pos_emb)

        hiddens.append(core_out)

        for i, layer in enumerate(self.layers):
            mems_i = None if mems is None else mems[i]
            core_out = layer(core_out, pos_emb, self.r_w_bias, self.r_r_bias, dec_attn_mask=dec_attn_mask, mems=mems_i)
            hiddens.append(core_out)

        core_out = self.drop(core_out)

        new_mems = self._update_mems(hiddens, mems, mlen, qlen)

        return core_out, new_mems

    def forward(self, x, y, *mems):
        if not mems: mems = self.init_mems()

        tgt_len = y.size(0)
        hidden, new_mems = self._forward(x, mems=mems)
        pred_hid = hidden[-tgt_len:]


class RelPartialLearnableDecLayer(nn.Module):
    def __init__(self, d_model, n_head, d_head, d_inner, dropout, **kwargs):
        super(RelPartialLearnableDecLayer, self).__init__()
        self.dec_attn = RelPartialLearnableMHDPA(n_head, d_model, d_head, dropout, **kwargs)
        self.ffn = PositionwiseFF(d_model, d_inner, dropout, pre_lnorm=kwargs.get('pre_lnorm'))

    def forward(self, inp, r, r_w_bias, r_r_bias, dec_attn_mask=None, mems=None):
        out = self.dec_attn(inp, r, r_w_bias, r_r_bias, dec_attn_mask, mems)
        out = self.ffn(out)
        return out


class RelPartialLearnableMHDPA(nn.Module):
    def __init__(self, n_head, d_model, d_head, dropout, tgt_len=None, mem_len=None, pre_lnorm=False):
        super(RelPartialLearnableMHDPA, self).__init__()

        self.n_head = n_head
        self.d_model = d_model
        self.d_head = d_head
        self.dropout = dropout

        self.qkv_net = nn.Linear(d_model, 3 * n_head * d_head, bias=False)
        self.drop = nn.Dropout(p=dropout)
        self.dropatt = nn.Dropout(p=dropout)
        self.o_net = nn.Linear(n_head * d_head, d_model, bias=False)
        self.layer_norm = nn.LayerNorm(d_model)

        self.scale = 1 / (d_head ** .5)
        self.pre_ln = pre_lnorm
        # xl
        self.r_net = nn.Linear(self.d_model, self.n_head * self.d_head, bias=False)

    def _rel_shift(self, x, zero_triu=False):
        bsz, klen, n_head, d_head = x.size()
        zero_pad = torch.zeros((bsz, 1, n_head, d_head), device=x.device, dtype=x.dtype)
        x_padded = torch.cat((zero_pad, x), 1)  # bsz, klen+1, n_head, d_head
        x_padded = x_padded.view(klen + 1, bsz, n_head, d_head)
        x = x_padded[1:].view_as(x)

        if zero_triu:
            ones = torch.ones((x.size(0), x.size(1)))
            x = x * torch.tril(ones, x.size(1) - x.size(0))[:, :, None, None]
        return x

    def forward(self, w, r, r_w_bias, r_r_bias, attn_mask=None, mems=None):
        qlen, rlen, bsz = w.size(0), r.size(0), w.size(1)

        if mems is not None:
            cat = torch.cat((mems, w), 0)
            if self.pre_ln:
                w_heads = self.qkv_net(self.layer_norm(cat))
            else:
                w_heads = self.qkv_net(cat)

            r_head_k = self.r_net(r)
            w_head_q, w_head_k, w_head_v = torch.chunk(w_heads, 3, dim=-1)
            w_head_q = w_head_q[-qlen:]
        else:
            if self.pre_ln:
                w_heads = self.qkv_net(self.layer_norm(w))
            else:
                w_heads = self.qkv_net(w)
            r_head_k = self.r_net(r)
            w_head_q, w_head_k, w_head_v = torch.chunk(w_heads, 3, dim=-1)
        klen = w_head_k.size(0)

        w_head_q = w_head_q.view(qlen, bsz, self.n_head, self.d_head)  # qlen, bsz, n_head, d_head
        w_head_k = w_head_k.view(klen, bsz, self.n_head, self.d_head)  # memlen + qlen, bsz, n_head, d_head
        w_head_v = w_head_v.view(klen, bsz, self.n_head, self.d_head)  # memlen + qlen, bsz, n_head, d_head

        r_head_k = r_head_k.view(rlen, self.n_head, self.d_head)  # qlen x n_head x d_head

        rw_head_q = w_head_q + r_w_bias
        AC = torch.einsum('ibnd, jbnd->ijbn', (rw_head_q, w_head_q))

        rr_head_q = w_head_q + r_r_bias
        BD = torch.einsum('ibnd,jnd->ijbn', (rr_head_q, r_head_k))
        BD = self._rel_shift(BD)

        # qlen, klen, bsz, n_head
        attn_score = AC + BD
        attn_score.mul_(self.scale)

        if attn_mask is not None and attn_mask.any().item():
            if attn_mask.dim() == 2:
                attn_score = attn_mask.float().masked_fill(attn_mask[None, :, :, None], -float('inf')).type_as(
                    attn_score)
            elif attn_mask.dim() == 3:
                attn_score = attn_mask.float().masked_fill(attn_mask[:, :, :, None], -float('inf')).type_as(attn_score)

        attn_p = F.softmax(attn_score, -1)
        attn_p = self.dropatt(attn_p)

        attn_vec = torch.einsum('ijbn,jbnd->ibnd', (attn_p, w_head_v))

        attn_vec = attn_vec.contiguous().view(attn_vec.size(0), attn_vec.size(1), self.n_head * self.d_head)

        attn_out = self.o_net(attn_vec)
        attn_out = self.drop(attn_out)

        if self.pre_ln:
            out = w + attn_out
        else:
            out = self.layer_norm(w + attn_out)
        return out


class PositionwiseFF(nn.Module):
    def __init__(self, d_model, d_inner, dropout, pre_ln=False):
        self.d_model = d_model
        self.d_inner = d_inner
        self.dropout = dropout

        self.coreNet = nn.Sequential(
            nn.Linear(d_model, d_inner), nn.ReLU(inplace=True),
            nn.Dropout(dropout),
            nn.Linear(d_inner, d_model),
            nn.Dropout(dropout),
        )
        self.layer_norm = nn.LayerNorm(d_model)
        self.pre_ln = pre_ln

    def forward(self, inp):
        core_out = self.coreNet(inp)
        if self.pre_ln:
            out = core_out + inp
        else:
            out = self.layer_norm(inp + core_out)
        return out


class PositionEmbedding(nn.Module):
    """ R_{i-j} in Att_rel in xl """

    def __init__(self, d_emb):
        super(PositionEmbedding, self).__init__()
        self.d_emb = d_emb
        inv_freq = 1 / (10000 ** (torch.arange(.0, d_emb, 2.0) / d_emb))
        self.register_buffer('inv_freq', inv_freq)

    def forward(self, pos_seq, bsz=None):
        sinuisoid_inp = torch.ger(pos_seq, self.inv_freq)  # outer product

        if bsz is not None:
            return pos_seq[:, None, :].expand(-1, bsz, -1)
        else:
            return pos_seq[:, None, :]

Comparison with Shaw et. al(2018)

Relative positional representation (RPR) (Shaw et. al, 2018) merely leveraged relative postional embedding, throwing away the sinusoid hard encodings. The RPR term $\color{red}{a_{ij}^K}$ introduces the trainable parameters. See my attention blog ^[6] for more details.

• The terms in the numerator correspond to terms (a) and (b) in relative PE in Transformer-XL. It is obvious that RPR shows a lack of the (c) and (d) terms.

$$\begin{align} e_{ij} &= \frac{x_i W^Q (x_j W^K \color{red}{+a_{ij}^K})^T}{\sqrt{d_z}} \\ &= \frac{ \overbrace{x_i W^Q (x_jW^K)^T}^\text{(a)} + \overbrace{\color{green}{\pmb{x_iW^Q(a_{ij}^Q)^T}}}^\text{(b)}}{\sqrt{d_z}} \\ \alpha_{ij} &= \frac{\exp e_{ij}}{\sum_{k=1}^n \exp e_{ik}} \\ z_i &= \sum_{j=1}^n \alpha_{ij}(x_jW^V \color{red}{+ a_{ij}^V} )\\ \end{align}$$

R-Transformer

• Argument: multi-head attention only learn the global dependencies, but it ignores the inherent local structures.^[4]

LocalRNN

R-Transformer^[4] employs LocalRNN to model local structures, only focusing on local short-term dependencies with a local short sequence of length $M$: $x_{t-M-1}, x_{t-M-2}, \cdots, x_t$. The last hidden state $h_t$ is the representation of the local short sequences of a fixed length $M$.

• LocalRNNs pad $(M-1)$ positions before the start of a sequence.
• R-Transformers do not use any position embeddings.
• Here, the LocalRNN resembles the 1D ConvNets but the op for each window is not convolution. However, the conv op completely ignores the sequential information of positions within the local window.

Image source:^[4]

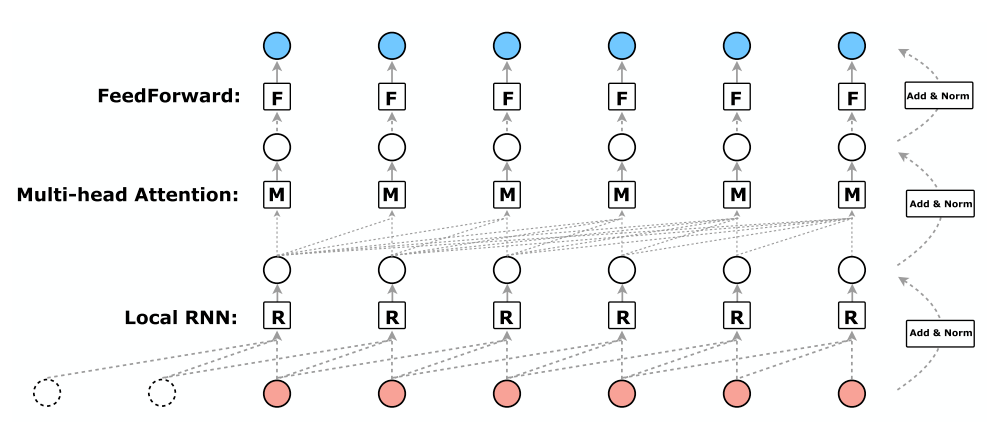
Given sequence of length $m$: $x_1, x_2, x_3, \cdots, x_m$ and window size $k=4$, localRNN encodes segmented short sub-sequence as:

$$\begin{align} &\text{the 1-st LocalRNN:} & \quad \text{<pad>}, \text{<pad>}, \text{<pad>}, x_1 \\ &\text{the 2-nd LocalRNN:} & \quad \text{<pad>}, \text{<pad>}, x_1, x_2 \\ &\text{the 3-rd LocalRNN:} & \quad \text{<pad>}, x_1, x_2, x_3 \\ &\text{the 4-th LocalRNN:} & \quad x_1, x_2, x_3, x_4 \\ &\text{the 5-th LocalRNN:} & \quad x_2, x_3, x_4, x_5 \\ &\text{the 6-th LocalRNN:} & \quad x_3, x_4, x_5, x_6 \\ & \cdots & \cdots\\ &\text{the m-th LocalRNN:} & \quad \underbrace{x_{m-3}, x_{m-2}, x_{m-1}, x_m}_\text{window size k=4} \end{align}$$

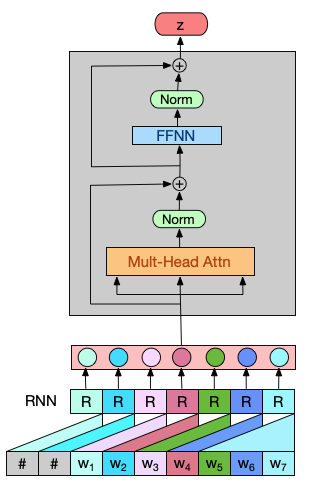
When doing implementation,

1. first pad the sequence with embeddings of all 0s on the left hand side (kernel size-1) positions;
2. then segment the subsequence of window size $k$, with one position shift right per time step. (See above digram.)

class LocalRNN(nn.Module):
    """ R transformer"""

    def __init__(self, input_size, output_size, window_size, rnn_type='GRU', MAX_LENGTH=10000):
        super(LocalRNN, self).__init__()
        self.window_size = window_size
        if rnn_type == 'GRU':
            # set `batch_first`=True so that the input and output dim are both (nBatch, seq_len, d_model)
            self.rnn = nn.GRU(output_size, output_size, batch_first=True)
        elif rnn_type == 'LSTM':
            self.rnn = nn.LSTM(output_size, output_size, batch_first=True)
        else:
            self.rnn = nn.RNN(output_size, output_size, batch_first=True)

        # generate segments according to window_size.
        # -> e.g. window size = 4, generate [1,2,3,4,
        #                                      2,3,4,5,
        #                                        3,4,5,6,
        #                                          4,5,6,7,
        #                                              ...
        #                                                  MAX_LEN - 1 -k ,... , MAX_LEN-2, MAX_LEN-1]
        idx = [i for j in range(window_size - 1, MAX_LENGTH) for i in range(j - (window_size - 1), j + 1)]
        self.idx = torch.LongTensor(idx)
        # padding (k-1) before the beginning of the sequence
        self.zeros_pad = torch.zeros((window_size - 1, input_size))

    def forward(self, x):
        """ regard window size dim as batch dim"""
        assert x.dim() == 3, '3 dimensions of input expected!'
        nbatches, seq_len, d_model = x.size()

        x = self._gather_seg_sequence(x)
        output, _ = self.rnn(x)
        h_last_per_batch = output[:, -1, :]
        return h_last_per_batch.view(nbatches, seq_len, d_model)

    def _gather_seg_sequence(self, x):
        nbatch, seq_len, d_model = x.size()
        # use `repeat` to pad one batch -> (nbatch, k01, input_size)
        zeros = self.zeros_pad.repeat(bsz, 1, 1)
        # concat padded zeros and the sequence along the sequence dim
        x = torch.cat((zeros, x), dim=1)
        # gather the corresponding embeddings along the sequence dim (1)
        idx = self.idx[:self.window_size * seq_len]  #
        x_ = torch.index_select(input=x, dim=1, index=idx)
        # reshape -> (bsz * seq_len, window_size, d_model)
        x_ = x_.reshape(nbatch * seq_len, self.window_size, -1)
        return x_
        
class SublayerConnection(nn.Module):
    """
    a residual connection followed by a layer norm
    """

    def __init__(self, size, dropout):
        super(SublayerConnection, self).__init__()
        self.norm = LayerNorm(size)
        self.dropout = nn.Dropout(dropout)

    def forward(self, x, sublayer):
        """ Apply residual connection to any sublayer with the same size"""
        return x + self.dropout(sublayer(self.norm(x)))

class LocalRNNLayer(nn.Module):
    def __init__(self, size, dropout=.0):
        super(LocalRNNLayer, self).__init__()
        self.local_rnn = LocalRNN(size, size, window_size=5)
        self.sublayer = SublayerConnection(size, dropout)

    def forward(self, x):
        return self.sublayer(x, self.local_rnn)

For $i$-th layer, ($i \in {1,2,\cdots,N}$)

$$\begin{align} h_1^i, h_2^i, \cdots, h_T^i &= \text{LocalRNN}(x_1^i, x_2^i, \cdots, x_T^i) \\ \hat{h}_1^i, \hat{h}_2^i, \cdots, \hat{h}_T^i &= \text{LayerNorm}(h_1^i + x_1^i, h_2^i+x_2^i, \cdots, h_T^i+x_T^i) \\ o_1^i,o_2^i,\cdots,o_T^{i} &= \text{Transformer-Layer}(\hat{h}_1^i, \hat{h}_2^i, \cdots, \hat{h}_T^i) \end{align}$$

References

---

1. 1.Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones, L., Gomez, A. N., ... & Polosukhin, I. (2017). Attention is all you need. In Advances in neural information processing systems (pp. 5998-6008). ↩
2. 2.Al-Rfou, R., Choe, D., Constant, N., Guo, M., & Jones, L. (2019, July). Character-level language modeling with deeper self-attention. In Proceedings of the AAAI Conference on Artificial Intelligence (Vol. 33, pp. 3159-3166). ↩
3. 3.Dai, Z., Yang, Z., Yang, Y., Cohen, W. W., Carbonell, J., Le, Q. V., & Salakhutdinov, R. (2019). Transformer-xl: Attentive language models beyond a fixed-length context. arXiv preprint arXiv:1901.02860. ↩
4. 4.Wang, Z., Ma, Y., Liu, Z., & Tang, J. (2019). R-Transformer: Recurrent Neural Network Enhanced Transformer. arXiv preprint arXiv:1907.05572. ↩
5. 5.Shaw, P., Uszkoreit, J., & Vaswani, A. (2018). Self-attention with relative position representations. arXiv preprint arXiv:1803.02155. ↩
6. 6.Attention in a nutshell! ↩
7. 7.Tensor2Tensor tensorflow code ↩
8. 8.TRANSFORMERS FROM SCRATCH ↩