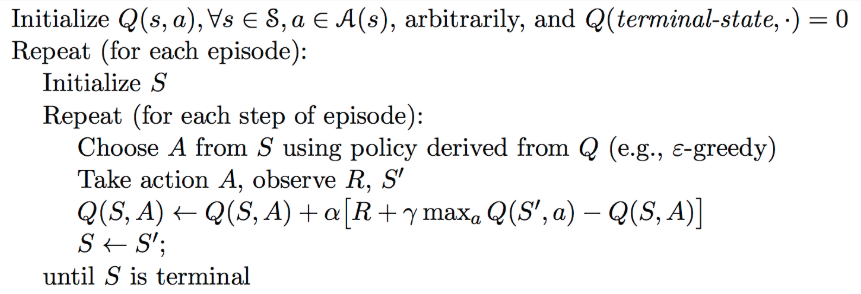Notes of lectures by D. Silver.
For problems like elevator, robot walking and the game of Go, MDP model is unknown, but experience can be sampled; or MDP model is known, but is too big to use, except by samples. Model-free control could solve this.
- On-policy learning
- “learn on the job“
- Learn about policy $\pi$ from experience sampled from $\pmb{\pi}$
- Off-policy learning
- “learn over someone’s shoulder“
- Learn about policy $\pi$ from experience sampled from $\pmb{\mu}$
On-policy
On-policy Monte-Carlo control
- Greedy policy improvement over $V(s)$ requires model of MDP:
- Greedy policy improvement over $Q(s,a)$ is model-free:
$\epsilon$-greedy exploration
- Simplest idea for ensuring continual exploration
- All $m$ actions are tried with non-zero probability
- With probability $1-\epsilon$ choose the greedy action
- With probability $\epsilon$ choose an action at random
On-policy Temporal-Difference learning
MC vs. TD control
- TD learning has several advantages over MC:
- Lower variance
- Online
- Incomplete sequences
- Natural idea: use TD instead of MC in out control loop
- Apply TD to $Q(S,A)$
- Use $\epsilon$-greedy policy improvement
- Update every time-step
Sarsa($\lambda$)
SARSA:

Every time-step:
- Policy evaluation Sarsa:
- Policy improvement $\epsilon$-greedy policy improvement
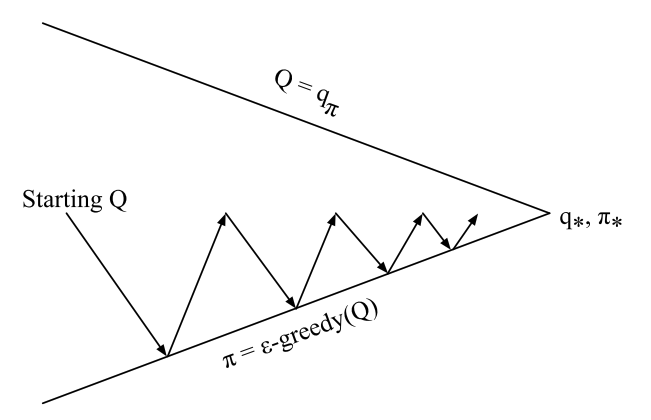

$n$-step Sarsa
- Consider the following $n$-step returns for $n=1,2,\infty$
Define the $n$-step Q-return
$n$-step Sarsa updates $Q(s,a)$ towards the n-step Q-return
Forward-view Sarsa($\lambda$)
- The $q^{\pi}$ return combines all $n$-step Q-returns
- Using weight $(1-\lambda) \lambda^{(n-1)}$
- Forward-view Sarsa($\lambda$)
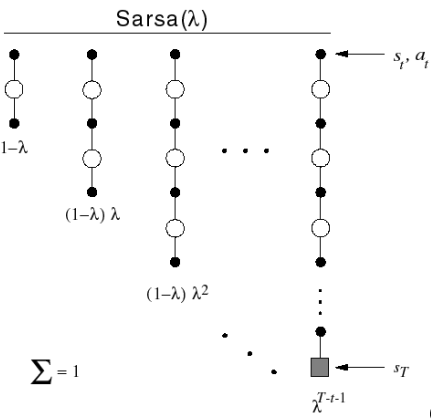
Back-view Sarsa($\lambda$)
- Like TD($\lambda$), we use eligibility traces
- Sarsa($\lambda$) has one eligibility trace for each state-action pair
- $Q(s,a)$ is updated for every state $s$ and action $a$
- In proportion to TD-error and eligibility trace

Off-policy learning
Off-policy control with Q-learning