Model-Free Prediction (RL)

Notes of lectures by D. Silver.

Monte-Carlo Learning

• MC methods learn directly from episodes of experience
• MC is model-free: no knowledge of MDP transitions / rewards.
• MC learns from complete episodes: no bootstrapping
• MC uses the simplest possible idea: value = mean return
• Caveat: can only apply MC to episodic MDPs
  • All episodes must terminate

MC policy evaluation

• Goal： learn $v_{\pi}$ from episodes of experience under policy $\pi$ $$S_1, A_1, R_2, \cdots , S_k \sim \pi$$
• The return is the total discounted reward: $$G_t = R_{t+1} + \gamma R_{t+2} + \cdots + \gamma^{T-1} R_T$$
• The value function is the expected return: $$v_{\pi}(s) = \mathbb{E}_{\pi}[G_t \vert S_t = s]$$
• Monte-Carlo policy evaluation uses empirical mean return instead of expected return

First-visit MC policy evaluation

To evaluate state $s$

• The first time-step $t$ that state $s$ is visited in an episode
• Increment counter $N(s) \leftarrow N(s) + 1$
• Increment counter $S(s) \leftarrow S(s) + G_t$
• Value is estimated by mean return $V(s) = S(s) / N(s)$
• By law of large numbers, $V(s) \rightarrow v_{\pi}(s)$ as $N(s) \rightarrow \infty$

Every-visit MC policy evaluation

To evaluate state $s$

• The every time-step $t$ that state $s$ is visited in an episode
• Increment counter $N(s) \leftarrow N(s) + 1$
• Increment counter $S(s) \leftarrow S(s) + G_t$
• Value is estimated by mean return $V(s) = S(s) / N(s)$
• By law of large numbers, $V(s) \rightarrow v_{\pi}(s)$ as $N(s) \rightarrow \infty$

Incremental Monte-Carlo

Incremental Mean

The mean $\mu_1, \mu_2, \cdots$ of a sequence $x_1, x_2, \cdots$ can be computed incrementally

$$\mu_k = \frac{1}{k} \sum_{j=1}^k x_j \\ =\frac{1}{k} \big( x_k + \sum_{j=1}^{k-1}x_j \big) \\ =\frac{1}{k} \big( x_k + (k-1) \mu_{k-1} \big) \\ = \mu_{k-1} + \frac{1}{k} (x_k - \mu_{k-1})$$

Incremental MC updates

• Update $V(s)$ incrementally after episode $S_1, A_1, R_2, \cdots, S_T$
• For each state $S_t$ with return $G_t$ $$N(S_t) \leftarrow N(S_t) + 1$$ $$V(S_t) \leftarrow V(S_t) + \frac{1}{N(S_t)} (G_t - V(S_t))$$
• In non-stationary problems, it can be useful to track a running mean, i.e. forget old episodes $$V(S_t) \leftarrow V(S_t) + \alpha (G_t - V(S_t))$$

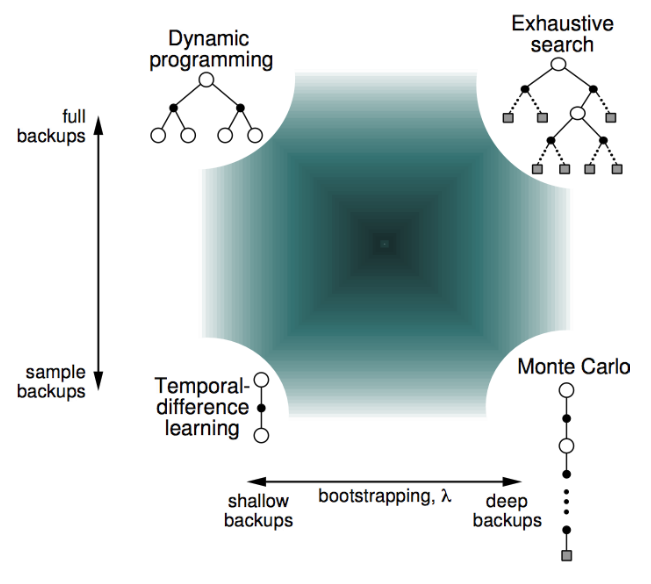
Temporal-Difference Learning

• TD methods learn directly from episodes of experience
• TD is model-free: no knowledge of MDP transitions / rewards
• TD learns from incomplete episodes, by bootstrapping
• TD updates a guess towards a guess

MC and TD

• goal: learn $v_{\pi}$ online from experience under policy $\pi$

• Incremental every-visit MC

  • Update value $V(S_t)$ toward actual return $G_t$

    $$V(S_t) \leftarrow V(S_t) + \alpha (G_t - V(S_t))$$
• Simplest temporal-difference learning algorithm: TD(0)
  • Update $V(S_t)$ toward estimated return $R_{t+1} + \gamma V(S_{t+1})$ $$V(S_t) \leftarrow V(S_t) +\alpha \underbrace{(\overbrace{\pmb{R_{t+1} + \gamma V(S_{t+1})}}^\text{TD target} - V(S_t) )}_\text{TD error}$$

MC v.s TD

Pros and cons

1.Process

• TD can learn before knowing the final outcome

  • TD can learn online after every step
  • MC must wait until end of episode before return is known

• TD can learn without the final outcome

  • TD can learn from incomplete sequences
  • MC can only learn from complete sequences
  • TD works in continuing (non-terminating) environments
  • MC only works for episodic (terminating) environments

2.Statistics

• MC has high variance, zero bias
  • Good convergence properties (even with function approximation)
  • Not very sensitive to initial value
  • Very simple to understand and use
• TD has low variance, some bias
  • Usually more efficient than MC
  • TD(0) converges to $v_{\pi}(s)$ but not always with function approximation
  • More sensitive to initial value

3.Markov property

• TD exploits Markov property
  • Usually more efficient in Markov environments
• MC does not exploit Markov property
  • Usually more efficient in non-Markov environments

Bias / Variance trade-off

• Return $G_t = R_{t+1} + \gamma R_{t+2} + \cdots + \gamma^{T-1} R_{T}$ is unbiased estimate of $v_{\pi}(S_t)$
• True TD target $T_{t+1} + \gamma v_{\pi}(S_{t+1})$ is unbiased estimate of $v_{\pi}(S_t)$
• TD target $R_{t+1} + \gamma V(S_{t=1})$ is biased estimate of $v_{pi}(S_t)$
• TD target is much lower variance that the return:
  • Return depends on many random actions, transitions, rewards
  • TD target depends on one random action, transition, reward