An Introduction to Capsules

A capsule is defined as a group of neuron instantiations whose parameters represent specific properties of a specific type of entity. Here is a brief note of Capsule networks^[1][2].

Convolutional Neural Networks (CNNs) extract local-region features with fixed strides, followed by max-pooling, which may only retain the remarkable features but ignore the fine-grain features such as overlapping entities in images. Capsules are regarded as a better solution to handle this.

Capsules with dynamic routing

Standard inputs and outputs of neural layers are scalar features, while Capsule Networks leverage capsules of vectors to represent features of entities.

Capsule

For each capsule, the input $\mathbf{u}_i$ and the output $\mathbf{v}_j$ are vectors.^[1]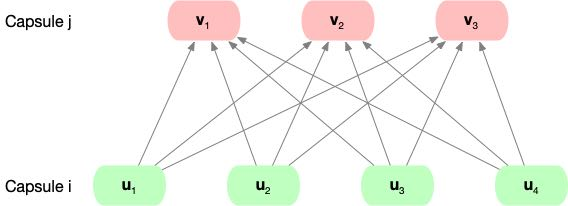

For all except the first layer of capsules, the input to a capsule $\mathbf{s}_j$ is a weighted sum over all “predicted vector” $\hat{\mathbf{u}}_{j \vert i}$, which is linearly transformed with a learnable weight matrix $\mathbf{W}_{ij}$.

$$\begin{align} \hat{\mathbf{u}}_{j \vert i} &= \mathbf{W}_{ij} \mathbf{u}_i \\ \mathbf{s}_j &= \sum_i c_{ij} \hat{\mathbf{u}}_{j \vert i} \end{align}$$

where coupling coefficients $c_{ij}$ between capsule $i$ and all all capsules in the layer above are scaled with a “routing softmax” to sum to 1. We will introduce this in the next section.

A squashing activation function rather than ReLU is used on $\mathbf{s}_j$, ensuring that the short and long vectors to approach to the length of almost zero and slighly below 1, respectively.

$$\mathbf{v}_j = \frac{\Vert \mathbf{s}_j \Vert^2}{1 + \Vert \mathbf{s}_j \Vert^2} \frac{\mathbf{s}_j}{\Vert \mathbf{s}_j \Vert}$$

Here $\mathbf{v}_j \rightarrow \Vert \mathbf{s}_j \Vert \mathbf{s}_j$ for $\mathbf{s}_j$ is too small, while $\mathbf{v}_j \rightarrow \frac{\mathbf{s}_j}{\Vert \mathbf{s}_j \Vert}$ when that is large.

The weight $c_{ij}$ is computed with iteration:

$$c_{ij} = \frac{\exp (b_{ij})}{\sum_{k} \exp(b_{ik})}$$

where the log probabilities $b_{ij}$ measure the probability that capsule $i$ should be coupled to capsule $j$ above, and are iteratively updated with:

$$\begin{align} a_{ij} &= \hat{\mathbf{u}}_{j \vert i} \cdot \mathbf{v}_j \\ b_{ij} &\leftarrow b_{ij} + a_{ij} \end{align}$$

where $a_{ij}$ measures the agreement between the current output $\mathbf{v}_j$ of capsule $j$ in above layer and $\hat{\mathbf{u}}_{j \vert i}$ in capsule $i$.

Dynamic routing

Margin loss

For each capsule $k$, seperate margin loss $L_k$ is:

$$L_k = T_k \max(0, m^+ - \Vert \mathbf{v}_k \Vert^2) + \lambda (1-T_k) \max(0, \Vert \mathbf{v}_k \Vert - m^-)^2$$

where $T_k=1$ iff class $k$ is present, $m^+ =0.9, m^-=0.1, \lambda = 0.5$. The total loss just simply sum all capsules.

Matrix capsules with EM routing

Capsules consist of a pose matrix $\mathbf{M} \in \mathbb{R}^{4 \times 4}$ and an activation probability $a \in \mathbb{R}$. Expectation-Maximization algorithm is used to iteratively update the cluster of capsules with similar votes.

Let we denote the capsules in layer $L$ as $\Omega_L$, trainable weights between each capsule $i$ in layer $i$ and each capsule $j$ in layer $L+1$ as $\mathbf{W}_{ij} \in \mathbb{R}^{4 \times 4}$.

$$\mathbf{V}_{ij}= \mathbf{M}_i \mathbf{W}_{ij}$$

The iterative update of pose matrix and activations of all capsules in layer $L+1$ leverages a non-linera routing procedure to get input $\mathbf{V}_{ij}$ and $a_i$ for all $i \in \Omega_L, j \in \Omega_{L+1}$.

Spread loss

Spread loss directly maximizes the gap between the activation of the target class $a_t$ and the activation of other classes.

$$\begin{align} L_i &= (\max(0, m- (a_t - a_i)))^2 \\ L &= \sum_{i \neq t} L_i \end{align}$$

where $m = 0.2$ initially and linearly increases during training to 0.9, equal to squared Hinge loss with $m=1$.

References

---

1. 1.Sabour, S., Frosst, N. and Hinton, G.E., 2017. Dynamic routing between capsules. In Advances in neural information processing systems (pp. 3856-3866). ↩
2. 2.Hinton, G.E., Sabour, S., and Frosst, N., 2018. Matrix capsules with EM routing. ↩
3. 3.Blog: Understanding Dynamic Routing between Capsules ↩
4. 4.Blog: Understanding Matrix capsules with EM Routing ↩
5. 5.FreeCodeCamp: Understanding Capsule Networks ↩
6. 6.TensorFlow code ↩