Graph Neural Networks (GNNs) has demonstrated efficacy on non-Euclidean data, such as social media, bioinformatics, etc.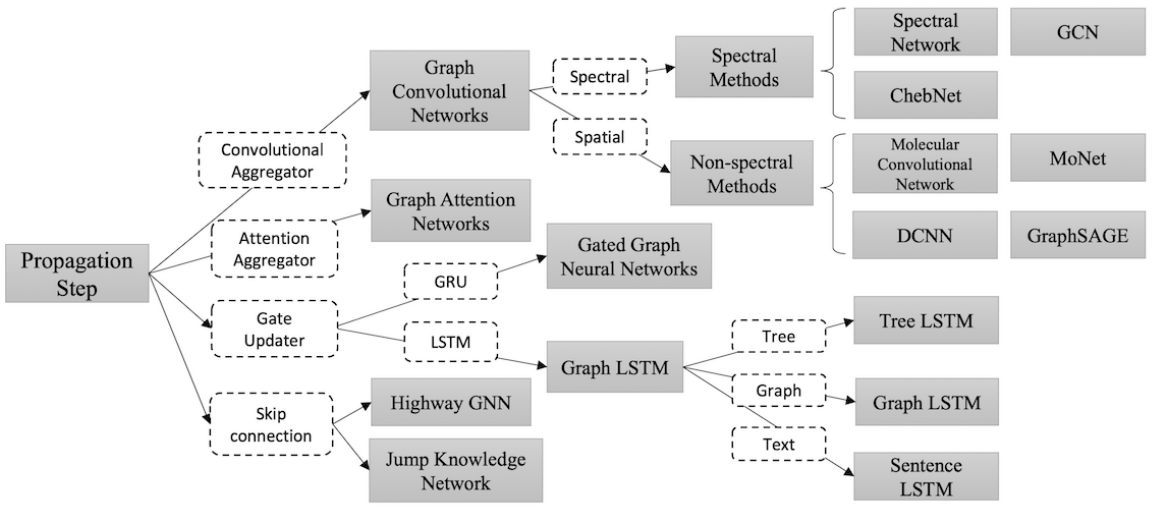
Related background
Convolution
Denoting $g$ as the filter on $f$, the convolution:
Fourier transformation
- Fourier transformation:
Inverse Fourier transformation:
The convolution can be rewritten as:
Spectral methods
Graph Convolutional Networks (GCN)
GCN[2] applies convolutions in the Fourier domain by computing the eigendecomposition of the graph Lapacian [3] using the first-order approximation. When applying convolution on the signal $x$ with the filter parameterized by $\theta \in \mathbb{R}^N$ in the Fourier domain, i.e.,
where $U$ is the matrix of eigenvectors of the normalized graph Laplacian
Let , we get:
Source code (TensorFlow)
Source code (PyTorch)
- spectral convolution can only be applied on undirected graphs, assuring that $L$ is a symmetric matrix.
Non-spectral methods
GraphSAGE
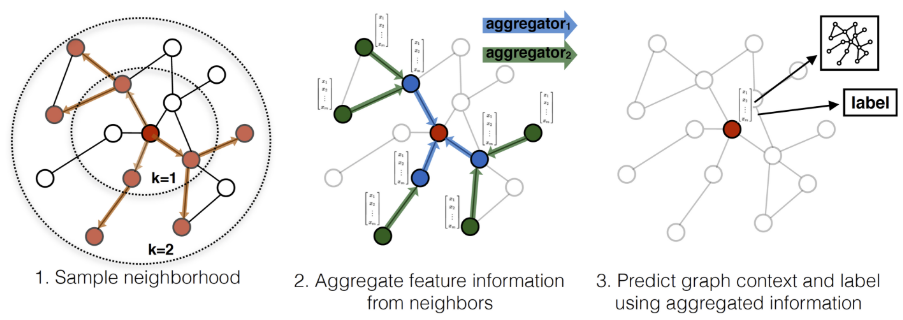
GraphSAGE is one of the archetype of non-spatial approaches. It samples from the neighborhood in the graph and aggregates the feature information from its local neighborhood.[4]

Graph Attention Networks (GAT)
Notation:
- Input (node features): , where $N$ is the # of nodes, $F$ is the # of features in each node.
- Output: , where $F^\prime$ is the output dimension.
- Pass inputs $\mathbf{h}$ into a learnable shared linear transformation, parameterized by a weight matrix $\mathbf{W} \in \mathbb{R}^{F^\prime \times F}$.
![]()
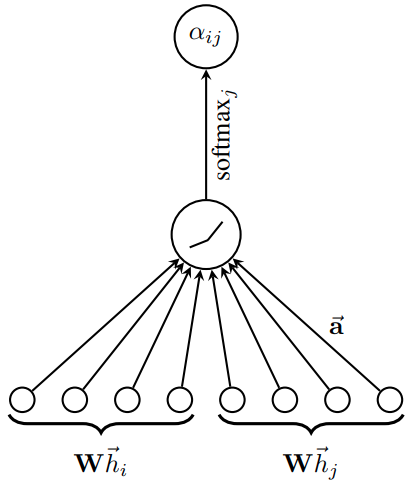
- Perform self-attention on the nodes
- compute the attention coefficients using a shared attention mechanism $a: \mathbf{R}^{F^\prime \times F} \rightarrow \mathbf{R}$:
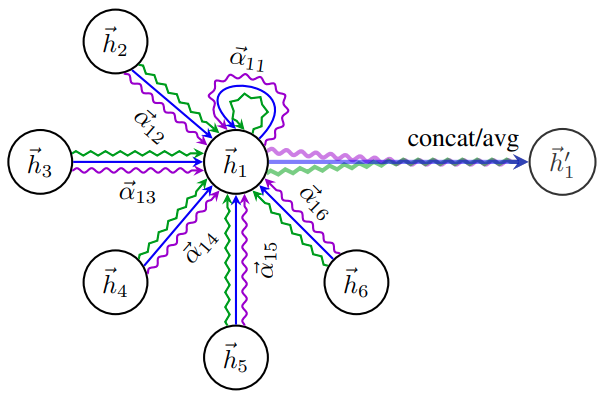
- Compute for nodes ,where is the neighborhood of node $i$ (including $i$) in the graph. Let $\Vert$ denote concatenation,
- Multi-head attention. The final output dimension is , where $k$ is the attention number.
- For the final layer, GAT aggregates neighbor nodes by averaging different node representations:
Graph Transformer Networks (GTN)
References
- 1.Zhou, J., Cui, G., Zhang, Z., Yang, C., Liu, Z., & Sun, M. (2018). Graph Neural Networks: A Review of Methods and Applications. ArXiv, abs/1812.08434. ↩
- 2.Kipf, T., & Welling, M. (2016). Semi-Supervised Classification with Graph Convolutional Networks. ArXiv, abs/1609.02907. ↩
- 3.Laplacian matrix wiki ↩
- 4.Hamilton, W.L., Ying, Z., & Leskovec, J. (2017). Inductive Representation Learning on Large Graphs. NIPS. ↩
- 5.Velickovic, P., Cucurull, G., Casanova, A., Romero, A., Liò, P., & Bengio, Y. (2018). Graph Attention Networks. ICLR ↩
- 6.Yun, S., Jeong, M., Kim, R., Kang, J., & Kim, H.J. (2019). Graph Transformer Networks. NeurIPS. ↩