This is an introduction of recent BERT families.

Relevant notes:

LM pretraining background

Autoregressive Language Modeling

Given a text sequence $\pmb{x} = (x_1, \cdots, x_T)$ , autoregressive (AR) language modeling factorizes the likelihood along a uni direction according to the product rule, either forward:

$p(\pmb{x})=\prod_{t=1}^T p(x_t \vert x_{<t}))$

or backward:

$p(\pmb{x})=\prod_{t=T}^1 p(x_t \vert x_{>t}))$

The AR pretraining maximizes the likehood under the forward AR factorization:

$\begin{align} \max_\theta \log p_\theta (\pmb{x}) &= \sum_{t=1}^T \log p_\theta (x_t \vert \pmb{x}_{<t}) \\ & = \sum_{t=1}^T \log \frac{\exp\left( \overbrace{h_\theta (\pmb{x}_{1:t-1})^T}^\text{context representation } \overbrace{e(x_t)}^\text{ embedding} \right)}{\sum_{x'}\exp\left( h_\theta (\pmb{x}_{1:t-1})^T e(x') \right)} \end{align}$

where $h_\theta (\pmb{x}_{1:t-1})$ denotes the context representation by NNs, such as RNNs/Transformers; $e(x_t)$ denotes the embedding of $x$.

It is not effective to model the deep bidirectional contexts.

Autoencoding based pretraining

Autoencoding (AE) based pretraining does not perform density estimation, but recover the original data from corrupted (masked) input.

Denosing autoencoding based pretraining, such as BERT can model the bidirectional contexts. Given a text sequence $\pmb{x} = (x_1, \cdots, x_T)$ , it randomly masks a portion (15%) of tokens $\bar{\pmb{x}}$ in $\pmb{x}$. The training objective is to reconstruct randomly masked token $\bar{\pmb{x}}$ from corrupted sequence $\hat{\pmb{x}}$:

$\begin{align} \max_\theta \log p_\theta (\bar{\pmb{x}} \vert \hat{\pmb{x}}) & \approx \sum_{t=1}^T m_t \log p_\theta (x_t \vert \hat{\pmb{x}}) \\ & = \sum_{t=1}^T m_t \log \frac{\exp\big( H_\theta (\hat{\pmb{x}})^T_t e(x_t) \big)}{\sum_{x'} \exp\big( H_\theta(\hat{\pmb{x}})_t^T e(x') \big)} \end{align}$

where

$m_t=1$ means $x_t$ is masked;
the Transformer $H_\theta$ encodes $\pmb{x}$ into hidden vectors $H_\theta(\pmb{x}) = \big[H_\theta(\pmb{x})_1, H_\theta(\pmb{x})_2, \cdots, H_\theta(\pmb{x})_T \big]$

However, it relies on corrupting the input with masks. The drawbacks:

Independent assumption: cannot model joint probability and assume the predicted tokens are independent of each other. It neglects the dependency between the masked positions
pretrain-finetune discrepancy (input noise): the artificial symbols like [MASK] used by BERT does not exist during the training of downstream tasks.

XLNet

XLNet^[1] (CMU & Google brain 2019) leverages both the advatage of AR and AE LM objectives and hinder their drawbacks.

The permutation of the factorization order impedes the dependency between masked positions in BERT and still remains the AR-like objectives so as to prevent the pretrain-finetuning discrepancy.
On the other hand, with permutation, it attends to the bi-contextual information as in BERT.

Permutation Language Model

XLNet^[13] applies permutation language model by autoregressively pretraining bidirectional contexts by maximizing the expected likelihood over all permutations of the input sequence factorization order.

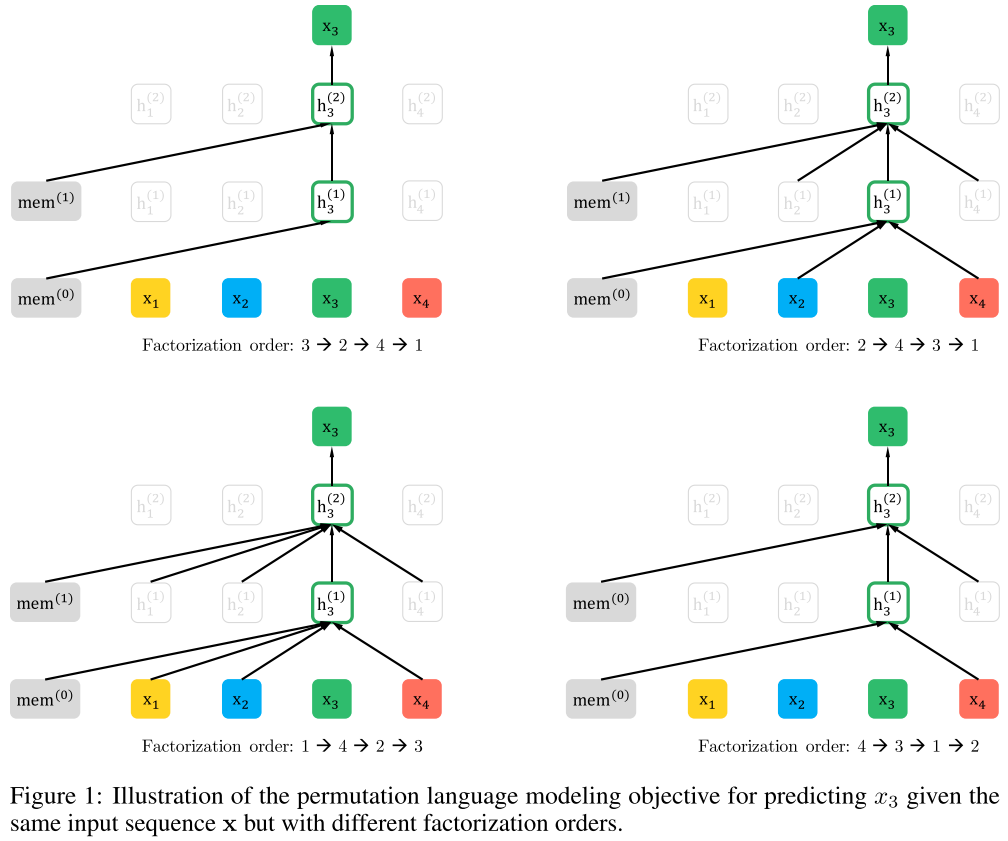
For a sequence $\pmb{x}$ of length $T$, there are $T!$ different orders to perform a valid AR factorization.

$\max_\theta \mathbb{E}_{\pmb{z}\sim Z_T} \left[ \sum_{t=1}^T \log p_\theta(x_{z_t} \vert \pmb{x}_{z<t}) \right]$

Permutation language modeling not only retains the benefits of AR models but also capture the bidirectional contexts as BERT. It only permutes the factorization order, rather than the sequence order.

Implementation

XLNet Implementation

# XLNet implementation (tf)
def _local_perm(inputs, targets, is_masked, perm_size, seq_len):
  """
  Sample a permutation of the factorization order, and create an
  attention mask accordingly.
  Args:
    inputs: int64 Tensor in shape [seq_len], input ids.
    targets: int64 Tensor in shape [seq_len], target ids.
    is_masked: bool Tensor in shape [seq_len]. True means being selected
      for partial prediction.
    perm_size: the length of longest permutation. Could be set to be reuse_len.
      Should not be larger than reuse_len or there will be data leaks.
    seq_len: int, sequence length.
  """

  # Generate permutation indices
  index = tf.range(seq_len, dtype=tf.int64)
  index = tf.transpose(tf.reshape(index, [-1, perm_size]))
  index = tf.random_shuffle(index)
  index = tf.reshape(tf.transpose(index), [-1])

  # `perm_mask` and `target_mask`
  # non-functional tokens
  non_func_tokens = tf.logical_not(tf.logical_or(
      tf.equal(inputs, SEP_ID),
      tf.equal(inputs, CLS_ID)))

  non_mask_tokens = tf.logical_and(tf.logical_not(is_masked), non_func_tokens)
  masked_or_func_tokens = tf.logical_not(non_mask_tokens)

  # Set the permutation indices of non-masked (& non-funcional) tokens to the
  # smallest index (-1):
  # (1) they can be seen by all other positions
  # (2) they cannot see masked positions, so there won"t be information leak
  smallest_index = -tf.ones([seq_len], dtype=tf.int64)
  rev_index = tf.where(non_mask_tokens, smallest_index, index)

  # Create `target_mask`: non-funcional and maksed tokens
  # 1: use mask as input and have loss
  # 0: use token (or [SEP], [CLS]) as input and do not have loss
  target_tokens = tf.logical_and(masked_or_func_tokens, non_func_tokens)
  target_mask = tf.cast(target_tokens, tf.float32)

  # Create `perm_mask`
  # `target_tokens` cannot see themselves
  self_rev_index = tf.where(target_tokens, rev_index, rev_index + 1)

  # 1: cannot attend if i <= j and j is not non-masked (masked_or_func_tokens)
  # 0: can attend if i > j or j is non-masked
  perm_mask = tf.logical_and(
      self_rev_index[:, None] <= rev_index[None, :],
      masked_or_func_tokens)
  perm_mask = tf.cast(perm_mask, tf.float32)

  # new target: [next token] for LM and [curr token] (self) for PLM
  new_targets = tf.concat([inputs[0: 1], targets[: -1]],
                          axis=0)

  # construct inputs_k
  inputs_k = inputs

  # construct inputs_q
  inputs_q = target_mask

  return perm_mask, new_targets, target_mask, inputs_k, inputs_q

Huggingface Implementation

@dataclass
class DataCollatorForPermutationLanguageModeling(DataCollatorMixin):
    """
    Data collator used for permutation language modeling.
    - collates batches of tensors, honoring their tokenizer's pad_token
    - preprocesses batches for permutation language modeling with procedures specific to XLNet
    """

    tokenizer: PreTrainedTokenizerBase
    plm_probability: float = 1 / 6
    max_span_length: int = 5  # maximum length of a span of masked tokens
    return_tensors: str = "pt"

    def torch_call(self, examples: List[Union[List[int], Any, Dict[str, Any]]]) -> Dict[str, Any]:
        if isinstance(examples[0], (dict, BatchEncoding)):
            examples = [e["input_ids"] for e in examples]
        batch = _torch_collate_batch(examples, self.tokenizer)
        inputs, perm_mask, target_mapping, labels = self.torch_mask_tokens(batch)
        return {"input_ids": inputs, "perm_mask": perm_mask, "target_mapping": target_mapping, "labels": labels}

    def tf_call(self, examples: List[Union[List[int], Any, Dict[str, Any]]]) -> Dict[str, Any]:
        if isinstance(examples[0], (dict, BatchEncoding)):
            examples = [e["input_ids"] for e in examples]
        batch = _tf_collate_batch(examples, self.tokenizer)
        inputs, perm_mask, target_mapping, labels = self.tf_mask_tokens(batch)
        return {"input_ids": inputs, "perm_mask": perm_mask, "target_mapping": target_mapping, "labels": labels}

    def numpy_call(self, examples: List[Union[List[int], Any, Dict[str, Any]]]) -> Dict[str, Any]:
        if isinstance(examples[0], (dict, BatchEncoding)):
            examples = [e["input_ids"] for e in examples]
        batch = _numpy_collate_batch(examples, self.tokenizer)
        inputs, perm_mask, target_mapping, labels = self.numpy_mask_tokens(batch)
        return {"input_ids": inputs, "perm_mask": perm_mask, "target_mapping": target_mapping, "labels": labels}

    def torch_mask_tokens(self, inputs: Any) -> Tuple[Any, Any, Any, Any]:
        """
        The masked tokens to be predicted for a particular sequence are determined by the following algorithm:
            0. Start from the beginning of the sequence by setting `cur_len = 0` (number of tokens processed so far).
            1. Sample a `span_length` from the interval `[1, max_span_length]` (length of span of tokens to be masked)
            2. Reserve a context of length `context_length = span_length / plm_probability` to surround span to be
               masked
            3. Sample a starting point `start_index` from the interval `[cur_len, cur_len + context_length -
               span_length]` and mask tokens `start_index:start_index + span_length`
            4. Set `cur_len = cur_len + context_length`. If `cur_len < max_len` (i.e. there are tokens remaining in the
               sequence to be processed), repeat from Step 1.
        """
        import torch

        if self.tokenizer.mask_token is None:
            raise ValueError(
                "This tokenizer does not have a mask token which is necessary for permutation language modeling. Please add a mask token if you want to use this tokenizer."
            )

        if inputs.size(1) % 2 != 0:
            raise ValueError(
                "This collator requires that sequence lengths be even to create a leakage-free perm_mask. Please see relevant comments in source code for details."
            )

        labels = inputs.clone()
        # Creating the mask and target_mapping tensors
        masked_indices = torch.full(labels.shape, 0, dtype=torch.bool)
        target_mapping = torch.zeros((labels.size(0), labels.size(1), labels.size(1)), dtype=torch.float32)

        for i in range(labels.size(0)):
            # Start from the beginning of the sequence by setting `cur_len = 0` (number of tokens processed so far).
            cur_len = 0
            max_len = labels.size(1)

            while cur_len < max_len:
                # Sample a `span_length` from the interval `[1, max_span_length]` (length of span of tokens to be masked)
                span_length = torch.randint(1, self.max_span_length + 1, (1,)).item()
                # Reserve a context of length `context_length = span_length / plm_probability` to surround the span to be masked
                context_length = int(span_length / self.plm_probability)
                # Sample a starting point `start_index` from the interval `[cur_len, cur_len + context_length - span_length]` and mask tokens `start_index:start_index + span_length`
                start_index = cur_len + torch.randint(context_length - span_length + 1, (1,)).item()
                masked_indices[i, start_index : start_index + span_length] = 1
                # Set `cur_len = cur_len + context_length`
                cur_len += context_length

            # Since we're replacing non-masked tokens with -100 in the labels tensor instead of skipping them altogether,
            # the i-th predict corresponds to the i-th token.
            target_mapping[i] = torch.eye(labels.size(1))

        special_tokens_mask = torch.tensor(
            [self.tokenizer.get_special_tokens_mask(val, already_has_special_tokens=True) for val in labels.tolist()],
            dtype=torch.bool,
        )
        masked_indices.masked_fill_(special_tokens_mask, value=0.0)
        if self.tokenizer._pad_token is not None:
            padding_mask = labels.eq(self.tokenizer.pad_token_id)
            masked_indices.masked_fill_(padding_mask, value=0.0)

        # Mask indicating non-functional tokens, where functional tokens are [SEP], [CLS], padding, etc.
        non_func_mask = ~(padding_mask | special_tokens_mask)

        inputs[masked_indices] = self.tokenizer.mask_token_id
        labels[~masked_indices] = -100  # We only compute loss on masked tokens

        perm_mask = torch.zeros((labels.size(0), labels.size(1), labels.size(1)), dtype=torch.float32)

        for i in range(labels.size(0)):
            # Generate permutation indices i.e. sample a random factorisation order for the sequence. This will
            # determine which tokens a given token can attend to (encoded in `perm_mask`).
            # Note: Length of token sequence being permuted has to be less than or equal to reused sequence length
            # (see documentation for `mems`), otherwise information may leak through due to reuse. In this implementation,
            # we assume that reused length is half of sequence length and permutation length is equal to reused length.
            # This requires that the sequence length be even.

            # Create a linear factorisation order
            perm_index = torch.arange(labels.size(1))
            # Split this into two halves, assuming that half the sequence is reused each time
            perm_index = perm_index.reshape((-1, labels.size(1) // 2)).transpose(0, 1)
            # Permute the two halves such that they do not cross over
            perm_index = perm_index[torch.randperm(labels.size(1) // 2)]
            # Flatten this out into the desired permuted factorisation order
            perm_index = torch.flatten(perm_index.transpose(0, 1))
            # Set the permutation indices of non-masked (non-functional) tokens to the
            # smallest index (-1) so that:
            # (1) They can be seen by all other positions
            # (2) They cannot see masked positions, so there won't be information leak
            perm_index.masked_fill_(~masked_indices[i] & non_func_mask[i], -1)
            # The logic for whether the i-th token can attend on the j-th token based on the factorisation order:
            # 0 (can attend): If perm_index[i] > perm_index[j] or j is neither masked nor a functional token
            # 1 (cannot attend): If perm_index[i] <= perm_index[j] and j is either masked or a functional token
            perm_mask[i] = (
                perm_index.reshape((labels.size(1), 1)) <= perm_index.reshape((1, labels.size(1)))
            ) & masked_indices[i]

        return inputs.long(), perm_mask, target_mapping, labels.long()

    def tf_mask_tokens(self, inputs: Any) -> Tuple[Any, Any, Any, Any]:
        """
        The masked tokens to be predicted for a particular sequence are determined by the following algorithm:
            0. Start from the beginning of the sequence by setting `cur_len = 0` (number of tokens processed so far).
            1. Sample a `span_length` from the interval `[1, max_span_length]` (length of span of tokens to be masked)
            2. Reserve a context of length `context_length = span_length / plm_probability` to surround span to be
               masked
            3. Sample a starting point `start_index` from the interval `[cur_len, cur_len + context_length -
               span_length]` and mask tokens `start_index:start_index + span_length`
            4. Set `cur_len = cur_len + context_length`. If `cur_len < max_len` (i.e. there are tokens remaining in the
               sequence to be processed), repeat from Step 1.
        """
        from random import randint

        import numpy as np
        import tensorflow as tf

        if self.tokenizer.mask_token is None:
            raise ValueError(
                "This tokenizer does not have a mask token which is necessary for permutation language modeling. Please add a mask token if you want to use this tokenizer."
            )

        if tf.shape(inputs)[1] % 2 != 0:
            raise ValueError(
                "This collator requires that sequence lengths be even to create a leakage-free perm_mask. Please see relevant comments in source code for details."
            )

        labels = tf.identity(inputs)
        # Creating the mask and target_mapping tensors
        masked_indices = np.full(labels.shape.as_list(), 0, dtype=np.bool)
        labels_shape = tf.shape(labels)
        target_mapping = np.zeros((labels_shape[0], labels_shape[1], labels_shape[1]), dtype=np.float32)

        for i in range(len(labels)):
            # Start from the beginning of the sequence by setting `cur_len = 0` (number of tokens processed so far).
            cur_len = 0
            max_len = tf.shape(labels)[1]

            while cur_len < max_len:
                # Sample a `span_length` from the interval `[1, max_span_length]` (length of span of tokens to be masked)
                span_length = randint(1, self.max_span_length + 1)
                # Reserve a context of length `context_length = span_length / plm_probability` to surround the span to be masked
                context_length = int(span_length / self.plm_probability)
                # Sample a starting point `start_index` from the interval `[cur_len, cur_len + context_length - span_length]` and mask tokens `start_index:start_index + span_length`
                start_index = cur_len + randint(0, context_length - span_length + 1)
                masked_indices[i, start_index : start_index + span_length] = 1
                # Set `cur_len = cur_len + context_length`
                cur_len += context_length

            # Since we're replacing non-masked tokens with -100 in the labels tensor instead of skipping them altogether,
            # the i-th predict corresponds to the i-th token.
            target_mapping[i] = np.eye(labels_shape[1])
        masked_indices = tf.cast(tf.convert_to_tensor(masked_indices), dtype=tf.bool)
        target_mapping = tf.convert_to_tensor(target_mapping)
        special_tokens_mask = tf.convert_to_tensor(
            [
                self.tokenizer.get_special_tokens_mask(val, already_has_special_tokens=True)
                for val in labels.numpy().tolist()
            ],
        )
        special_tokens_mask = tf.cast(special_tokens_mask, dtype=tf.bool)
        masked_indices = masked_indices & ~special_tokens_mask
        if self.tokenizer._pad_token is not None:
            padding_mask = labels == self.tokenizer.pad_token_id
            masked_indices = masked_indices & ~padding_mask

        # Mask indicating non-functional tokens, where functional tokens are [SEP], [CLS], padding, etc.
        non_func_mask = ~(padding_mask | special_tokens_mask)

        inputs = tf.where(masked_indices, self.tokenizer.mask_token_id, inputs)
        labels = tf.where(masked_indices, labels, -100)  # We only compute loss on masked tokens

        perm_mask = []

        for i in range(len(labels)):
            # Generate permutation indices i.e. sample a random factorisation order for the sequence. This will
            # determine which tokens a given token can attend to (encoded in `perm_mask`).
            # Note: Length of token sequence being permuted has to be less than or equal to reused sequence length
            # (see documentation for `mems`), otherwise information may leak through due to reuse. In this implementation,
            # we assume that reused length is half of sequence length and permutation length is equal to reused length.
            # This requires that the sequence length be even.

            # Create a linear factorisation order
            # tf.range is the equivalent of torch.arange
            perm_index = tf.range(labels_shape[1])
            # Split this into two halves, assuming that half the sequence is reused each time
            perm_index = tf.transpose(tf.reshape(perm_index, (-1, labels_shape[1] // 2)))
            # Permute the two halves such that they do not cross over
            perm_index = tf.random.shuffle(perm_index)  # Shuffles along the first dimension
            # Flatten this out into the desired permuted factorisation order
            perm_index = tf.reshape(tf.transpose(perm_index), (-1,))
            # Set the permutation indices of non-masked (non-functional) tokens to the
            # smallest index (-1) so that:
            # (1) They can be seen by all other positions
            # (2) They cannot see masked positions, so there won't be information leak
            perm_index = tf.where(~masked_indices[i] & non_func_mask[i], -1, perm_index)
            # The logic for whether the i-th token can attend on the j-th token based on the factorisation order:
            # 0 (can attend): If perm_index[i] > perm_index[j] or j is neither masked nor a functional token
            # 1 (cannot attend): If perm_index[i] <= perm_index[j] and j is either masked or a functional token
            perm_mask.append(
                (tf.reshape(perm_index, (labels_shape[1], 1)) <= tf.reshape(perm_index, (1, labels_shape[1])))
                & masked_indices[i]
            )
        perm_mask = tf.stack(perm_mask, axis=0)

        return tf.cast(inputs, tf.int64), tf.cast(perm_mask, tf.float32), target_mapping, tf.cast(labels, tf.int64)

    def numpy_mask_tokens(self, inputs: Any) -> Tuple[Any, Any, Any, Any]:
        """
        The masked tokens to be predicted for a particular sequence are determined by the following algorithm:
            0. Start from the beginning of the sequence by setting `cur_len = 0` (number of tokens processed so far).
            1. Sample a `span_length` from the interval `[1, max_span_length]` (length of span of tokens to be masked)
            2. Reserve a context of length `context_length = span_length / plm_probability` to surround span to be
               masked
            3. Sample a starting point `start_index` from the interval `[cur_len, cur_len + context_length -
               span_length]` and mask tokens `start_index:start_index + span_length`
            4. Set `cur_len = cur_len + context_length`. If `cur_len < max_len` (i.e. there are tokens remaining in the
               sequence to be processed), repeat from Step 1.
        """
        from random import randint

        import numpy as np

        if self.tokenizer.mask_token is None:
            raise ValueError(
                "This tokenizer does not have a mask token which is necessary for permutation language modeling. Please add a mask token if you want to use this tokenizer."
            )

        if inputs.shape[1] % 2 != 0:
            raise ValueError(
                "This collator requires that sequence lengths be even to create a leakage-free perm_mask. Please see relevant comments in source code for details."
            )

        labels = np.copy(inputs)
        # Creating the mask and target_mapping tensors
        masked_indices = np.full(labels.shape, 0, dtype=np.bool)
        target_mapping = np.zeros((labels.shape[0], labels.shape[1], labels.shape[1]), dtype=np.float32)

        for i in range(labels.shape[0]):
            # Start from the beginning of the sequence by setting `cur_len = 0` (number of tokens processed so far).
            cur_len = 0
            max_len = labels.shape[1]

            while cur_len < max_len:
                # Sample a `span_length` from the interval `[1, max_span_length]` (length of span of tokens to be masked)
                span_length = randint(1, self.max_span_length + 1)
                # Reserve a context of length `context_length = span_length / plm_probability` to surround the span to be masked
                context_length = int(span_length / self.plm_probability)
                # Sample a starting point `start_index` from the interval `[cur_len, cur_len + context_length - span_length]` and mask tokens `start_index:start_index + span_length`
                start_index = cur_len + randint(0, context_length - span_length + 1)
                masked_indices[i, start_index : start_index + span_length] = 1
                # Set `cur_len = cur_len + context_length`
                cur_len += context_length

            # Since we're replacing non-masked tokens with -100 in the labels tensor instead of skipping them altogether,
            # the i-th predict corresponds to the i-th token.
            target_mapping[i] = np.eye(labels.shape[1])

        special_tokens_mask = np.array(
            [self.tokenizer.get_special_tokens_mask(val, already_has_special_tokens=True) for val in labels.tolist()],
            dtype=np.bool,
        )
        masked_indices[special_tokens_mask] = 0
        if self.tokenizer._pad_token is not None:
            padding_mask = labels == self.tokenizer.pad_token_id
            masked_indices[padding_mask] = 0.0

        # Mask indicating non-functional tokens, where functional tokens are [SEP], [CLS], padding, etc.
        non_func_mask = ~(padding_mask | special_tokens_mask)

        inputs[masked_indices] = self.tokenizer.mask_token_id
        labels[~masked_indices] = -100  # We only compute loss on masked tokens

        perm_mask = np.zeros((labels.shape[0], labels.shape[1], labels.shape[1]), dtype=np.float32)

        for i in range(labels.shape[0]):
            # Generate permutation indices i.e. sample a random factorisation order for the sequence. This will
            # determine which tokens a given token can attend to (encoded in `perm_mask`).
            # Note: Length of token sequence being permuted has to be less than or equal to reused sequence length
            # (see documentation for `mems`), otherwise information may leak through due to reuse. In this implementation,
            # we assume that reused length is half of sequence length and permutation length is equal to reused length.
            # This requires that the sequence length be even.

            # Create a linear factorisation order
            perm_index = np.arange(labels.shape[1])
            # Split this into two halves, assuming that half the sequence is reused each time
            perm_index = perm_index.reshape((-1, labels.shape[1] // 2)).T
            # Permute the two halves such that they do not cross over
            np.random.shuffle(perm_index)
            # Flatten this out into the desired permuted factorisation order
            perm_index = perm_index.T.flatten()
            # Set the permutation indices of non-masked (non-functional) tokens to the
            # smallest index (-1) so that:
            # (1) They can be seen by all other positions
            # (2) They cannot see masked positions, so there won't be information leak
            perm_index[~masked_indices[i] & non_func_mask[i]] = -1
            # The logic for whether the i-th token can attend on the j-th token based on the factorisation order:
            # 0 (can attend): If perm_index[i] > perm_index[j] or j is neither masked nor a functional token
            # 1 (cannot attend): If perm_index[i] <= perm_index[j] and j is either masked or a functional token
            perm_mask[i] = (
                perm_index.reshape((labels.shape[1], 1)) <= perm_index.reshape((1, labels.shape[1]))
            ) & masked_indices[i]

        return inputs.astype(np.int64), perm_mask, target_mapping, labels.astype(np.int64)

Two-stream self-attention

The next-token distribution with the standard softmax formulation:

$p_\theta(X_{z_t}=x \vert \pmb{x}_{\pmb{z}<t}) = \frac{\exp \big( e(x)^T h_\theta (\pmb{x}_{\pmb{z}<t}) \big)}{\sum_{x'}\exp \big( e(x')^T h_\theta (\pmb{x}_{\pmb{z}<t}) \big)}$

where $h_\theta(\pmb{z}_{\pmb{z}<t})$ , abbr. $h_{z_t}$ , denotes content representation, which encodes both context and $x_{z_t}$ itself, as hidden states in Transformer, i.e. standard self-attention, see below figure(a).

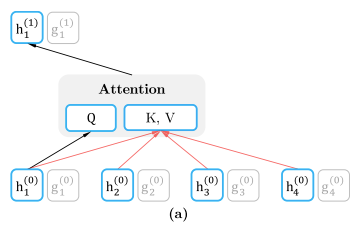
However, the previous $t-1$ sequence cannot implies the unique predicted target since different target words might have the same previous sequence in the permutated AR factorization. Hence, XLNet also consider the target position information:

$p_\theta(X_{z_t}=x \vert \pmb{x}_{z<t}) = \frac{\exp\left( e(x)^T g_\theta(\pmb{x}_{\pmb{z}<t}, \color{red}{z_t}) \right)}{\sum_{x'} \exp\left( e(x')^T g_\theta(\pmb{x}_{\pmb{z}<t}, \color{red}{z_t}) \right)}$

where $g_\theta(\pmb{x}_{\pmb{z}<t}, z_t)$ , abbr. $g_{z_t}$ denotes a query representation, only using the position $\color{red}{z_t}$ and not the context $\mathbf{x_{z_t}}$ , as below figure(b).

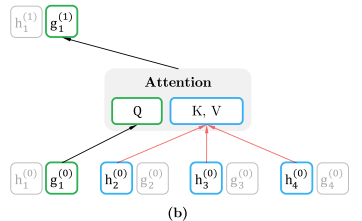
query stream uses $z_t$ but cannot see $x_{z_t}$ : $g_{z_t}^m \leftarrow \text{attention}\big(\pmb{Q}=g_{z_t}^{(m-1)}, \pmb{KV} = \pmb{h}_{\pmb{z}<t}^{(m-1)} ;\theta \big)$
content stream uses both $z_t$ and $x_{z_t}$ : $h_{z_t}^m \leftarrow \text{attention}\big(\pmb{Q}=h_{z_t}^{(m-1)}, \pmb{KV} = \pmb{h}_{\pmb{z}\leq t}^{(m-1)} ;\theta \big)$

Here $\pmb{Q}$,$\pmb{K}$,$\pmb{V}$ denot the query, key, value in an attention op.

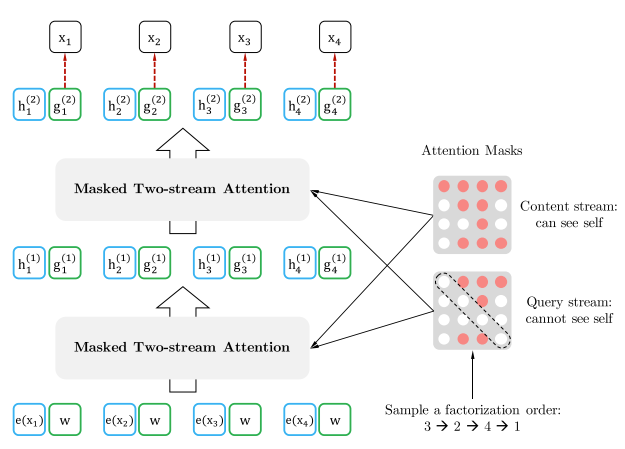
During finetuning, we can simply drop the query stream and use the content stream as a normal Transformer(-XL).
The permutation implementation is relying on the attention mask, as shown in the figure, which does not affect the original sequecen orders.

Transformer-XL

Borrow relative positional encoding and segment recurrence mechanism from Transformer-XL^[2].
The next segment with memory is:

$h_{z_t}^{(m)} \leftarrow \text{Att}( \mathbf{Q}= h_{z_t}^{(m-1)}, \, \mathbf{KV}= \big[ \mathbf{\tilde{h}}^{(m-1)}, \color{green}{\mathbf{h}_{z \leq t}^{(m-1)}} \big] ; \theta )$

Relative segment encoding

XLnet only considers ‘’whether the two positions in segments are within the same segment as opposed to considering which specific segments they are from‘’.

The idea of relative encodings is only modeling the relationships between positions $s_{ij}$ , denoting the segment encoding beween position i to j.
The attention weight $a_{ij} = (\mathbf{q}_i + \mathbf{b})^\top s_{ij}$ , where $\mathbf{q}_i$ is the query vector in std attention and $\mathbf{b}$ is a learnable head-specific bias vector. Finally add $a_{ij}$ to the normal attention weight.

The advantage of relative segment encodings:

to introduce inductive biases to improve generalization;
to allow for the multiple input segments in finetuning on tasks.

RoBERTa: “BERT is undertrained”!

RoBERTa^[5] (Fair & UW 2019) (Robustly optimized BERT approach) redesigned the BERT experiments^[6], illustrating BERT is underfitted. It showed that BERT pretraining with a larger batch size over more data for more training steps could lead to a better pretraining results.

Recent works^[1]^[5] questioned the effectiveness of Next Sentence Prediction (NSP) pretraining task proposed by BERT^[6].

SpanBERT

SpanBERT^[7] (UW & Fair) proposed a span-level pretraining approach by masking contiguous random spans rather than individual tokens as in BERT. It consistently surpass BERT and substantially outweights on span selection tasks involving question answering and coreference resolution. The NSP auxiliary objective is removed.

In comparison,

The concurrent work ERNIE^[8] (Baidu 2019) that masked linguistically-informed spans in Chinese, i.e. masking phrase and named entity, achieve improvements on Chinese NLP tasks.

Span masking

At each iteration, the span’s length is samplled from a geometric distribution $\mathscr{l} \sim Geo(p) = (1-p)^{(k-1)} p$; the starting point of spans are uniformly random selected from the sequence. (In SpanBERT, p=0.2, and clip $l_\max = 10$ .)

15% of tokens in span-level are masked: of which masking 80%, replacing 10% with noise, keeping the rest 10%.

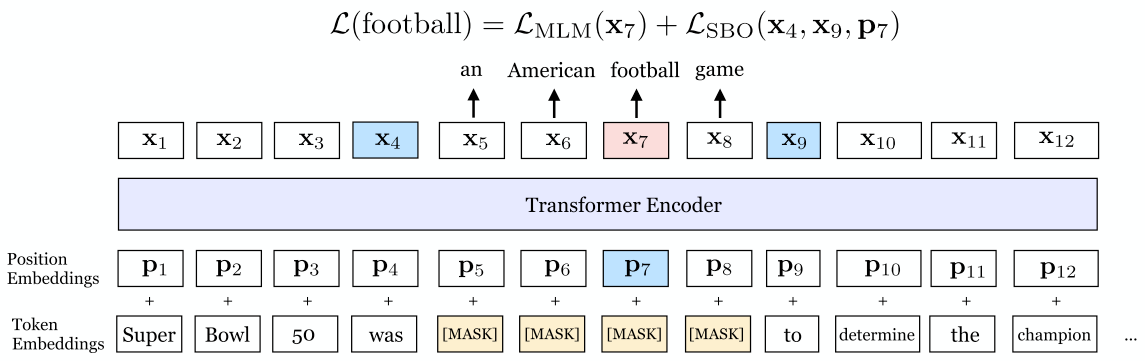
Span boundary objective (SBO)

Given a masked span $(x_s, \cdots, x_e) \in Y$ , where (s,e) denotes the start and ending positions. Each token $x_i$ in the span are represented using the encodings of the outside boundary tokens $x_{s-1}$ and $x_{e+1}$ (i.e., $x_4$ and $x_9$ in the figure) and the target positional embedding of target token $\mathbf{p}_i$ , that is:

$\mathbf{y}_i = f( \mathbf{x}_{s-1}, \mathbf{x}_{e+1}, \mathbf{p}_i)$

where $f(\cdot)$ indicates the 2-layer FFNN with layer normalizations and Gelu activations.

$\begin{align} \mathbf{h} & = \text{LayerNorm} (\text{Gelu} (W_q \cdot [\mathbf{x}_{s-1}; \mathbf{x}_{e+1}; \mathbf{p}_{i}] )) \\ f(\cdot) & = \text{LayerNorm} (\text{Gelu} (W_2 \cdot \mathbf{h})) \end{align}$

The representions of span tokens $\mathbf{y}_i$ is used to predict $\mathbf{x})i$ and compute the corss entropy loss like MLM objective in BERT.

ALBERT

ALBERT^[9] (A Lite BERT) (Google 2019) adopted factorized embedding parameterization and cross-layer parameter sharing techiniques to reuduce the memory cost of BERT architecture.

Factorized embedding parameterization

ALBERT decomposed the embedding parameters with higher dimension to smaller matrices, by firstly projecting the inputs into a lower dimensional embedding of size E, followed by the second projection to the hidden space. The embedding paprameters are reduced from $O(V \times H)$ to $O(V \times E + E \times H)$, which is obvious when $H \gg E$

All parameters across layers on both self-attentions and FFNs are shared. It is empirically showed that the L2 distance and cosine similarity between the input and output are oscillating rather than converging, which is different than that in Deep Equilibrium Model (DEQ)^[10].

Sentence-order prediction (SOP)

ALBERT use two consecutive setences as positive samples as in NSP, and swap the order of the same ajacent segments directly as the negative samples, consistently showing a better results for multi-sentence encoding tasks.

ELECTRA

ELECTRA^[11] (Efficiently Learning an Encoder that Classifies Token Replacements Accurately) (Standford NLP) proposed a more sample-efficient pre-training approach, replaced token detection to efficiently boost the pretraining efficiency, which solves the pretraining-finetuning discrepancy led by [MASK] symbols.

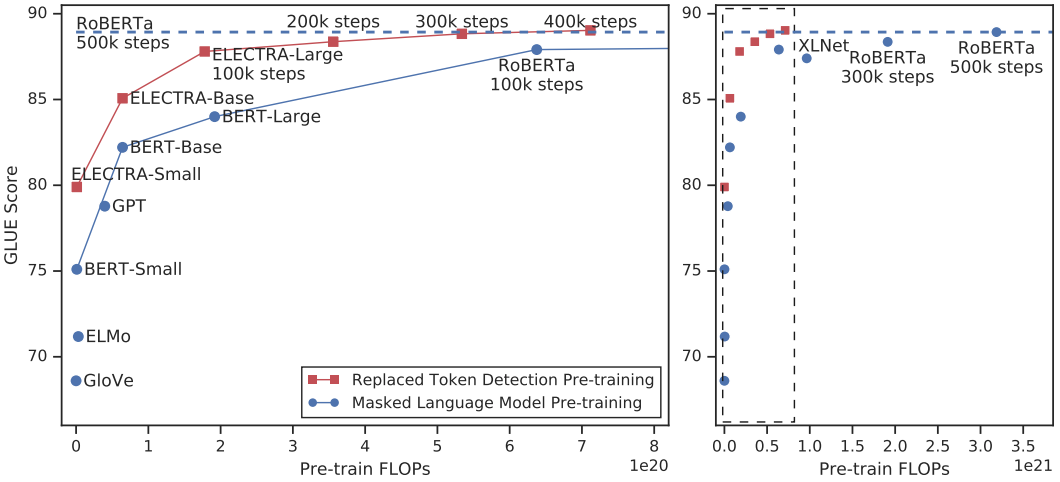
Replaced token detection

Rather than randomly masked tokens with the probability 15% as in BERT, replaced token detection replaces tokens with plausible alternatives that sampled from the output of a small generator network.
Then adopt a discriminator to predict whether each token was corrupted with a sampled replacement.

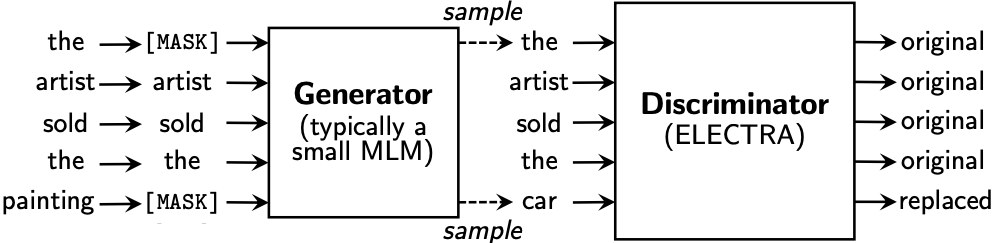
ELECTRA trains two NNs, a generator $G$ and a discriminator $D$. Each one primarily consists of an encoder that maps a sequence on input tokens $\mathbf{x}= [x_1,\cdots,x_n]$ into the contextual representation $h(\mathbf{x}) = [h_1, \cdots, h_n]$ .

The generator is used to to do Masked Language Model (MLM) as in BERT^[6]. For the position $t$, the generator outputs the distribution of $\mathbf{x}_t$ via a softmax layer:
$p_G (x_t \vert \mathbf{x}) = \frac{\exp (e(x_t)\top h_G(\mathbf{x})_t)}{\sum_{x^\prime} \exp(e(x^\prime)^\top h_G(\mathbf{x})_t)}$
where $e$ is the word embeddings.
For the discriminator $\mathscr{D}$, it discriminates whether the token $x_t$ at position $t$ is replaced.
$\mathscr{D}(\mathbf{x},t) = \sigma (w\top h_D(\mathbf{x})_t)$

MLM of BERT first randomly selects the positions to mask $\mathbf{m} = [m_1, \cdots, m_k]$ , wherein tokens at masked positions are replaced with a [MASK] token: $\begin{align}m_i &\sim \text{Uniform}\{1,n\} \\\mathbf{x}^\text{masked} &= \text{Replace}(\mathbf{x}, \mathbf{m}, \text{[MASK]})\end{align}$
In contrast, the replaced token detection uses the generator G to learn the MLE of masked tokens whilst the discriminator D is applied to detect the fakeness. $\begin{align}\color{red}{\hat{x}_i} &\sim p_G(x_i \vert \mathbf{x}^\text{masked}) \; \text{for}\, i\in \mathbf{m} \\\mathbf{x}^\text{corrupted} &= \text{Replace}(\mathbf{x}, \mathbf{m}, \color{red}{\hat{\mathbf{x}}})\end{align}$

Loss function

The loss functions are:

$\begin{align} \mathcal{L}_\text{MLM}(\mathbf{x}, \theta_G) &= \mathbb{E} \bigg( \sum_{i \in \mathbf{m}} - \log p_G (x_i \vert \mathbf{x}^\text{masked}) \bigg) \\ \mathcal{L}_\text{D} (\mathbf{x}, \theta_D) &= \mathbb{E} \bigg( \sum_{t=1}^n \mathbb{I} (x_t^\text{corrupt} = x_t) \log D(\mathbf{x}^\text{corrupt}, t) + \mathbb{I} (x_t^\text{corrupt} \neq x_t) \log ( 1- D\big(\mathbf{x}^\text{corrupt}, t\big) ) \bigg) \end{align}$

The combined loss is minimized:

$\min_{\theta_G, \theta_D} \sum_{\mathbb{x} \in \chi} \mathcal{L}_\text{MLM} (\mathbf{x}, \theta_G) + \lambda \mathcal{L}_\text{D}(\mathbf{x}, \theta_D)$

where $\chi$ denotes the corpus.

Training

Share the embeddings (both token embeddings and position embeddings) of the generator and discriminator.
Weight tying strategy^[12] -> only tied embeddings.

Two-stage training

Train only the geenrator with $\mathcal{L}_\text{MLM}$ for $n$ steps
Initialize the weights of the $D$ with $G$ and train $D$ with $\mathcal{L}_\text{Disc}$ for $n$ steps, keeping the generator’s weight frozen.

After pretraining, throw away the generator and fine-tune the discriminator on downstream tasks.

References

1.Yang, Z., Dai, Z., Yang, Y., Carbonell, J., Salakhutdinov, R., & Le, Q. V. (2019). XLNet: Generalized Autoregressive Pretraining for Language Understanding. arXiv preprint arXiv:1906.08237. ↩
2.Dai, Z., Yang, Z., Yang, Y., Cohen, W. W., Carbonell, J., Le, Q. V., & Salakhutdinov, R. (2019). Transformer-xl: Attentive language models beyond a fixed-length context. arXiv preprint arXiv:1901.02860. ↩
3.Shaw, P., Uszkoreit, J., & Vaswani, A. (2018). Self-attention with relative position representations. arXiv preprint arXiv:1803.02155. ↩
4.Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones, L., Gomez, A. N., ... & Polosukhin, I. (2017). Attention is all you need. In Advances in neural information processing systems (pp. 5998-6008). ↩
5.Liu, Y., Ott, M., Goyal, N., Du, J., Joshi, M., Chen, D., ... & Stoyanov, V. (2019). Roberta: A robustly optimized bert pretraining approach. arXiv preprint arXiv:1907.11692. ↩
6.Devlin, J., Chang, M. W., Lee, K., & Toutanova, K. (2018). Bert: Pre-training of deep bidirectional transformers for language understanding. arXiv preprint arXiv:1810.04805. ↩
7.Joshi, M., Chen, D., Liu, Y., Weld, D. S., Zettlemoyer, L., & Levy, O. (2019). Spanbert: Improving pre-training by representing and predicting spans. arXiv preprint arXiv:1907.10529. ↩
8.Sun, Y., Wang, S., Li, Y., Feng, S., Chen, X., Zhang, H., ... & Wu, H. (2019). ERNIE: Enhanced Representation through Knowledge Integration. arXiv preprint arXiv:1904.09223. ↩
9.Lan, Z., Chen, M., Goodman, S., Gimpel, K., Sharma, P., & Soricut, R. (2019). Albert: A lite bert for self-supervised learning of language representations. arXiv preprint arXiv:1909.11942. ↩
10.Deep Equilibrium Models. arXiv 2019 ↩
11.ELECTRA: Pre-training Text Encoders as Discriminators rather than Generators ↩
12.Press, O., & Wolf, L. (2016). Using the output embedding to improve language models. arXiv preprint arXiv:1608.05859. ↩
13.GitHub: XLNet ↩

Yekun's Note

BERTology: An Introduction!

LM pretraining background

Autoregressive Language Modeling

Autoencoding based pretraining

XLNet