Counting the Number of Parameters in Deep Learning

A guide to calculate the number of trainable parameters by hand.

Feed-forward NN

FFNN

$$y = X \cdot w^T + b$$

Given

• $\pmb{i}$ input size
• $\pmb{o}$ output size

For each FFNN layer

$$\begin{align} \text{the # of params} &= \text{connections between layers + biases of the layer} \\ &= (\pmb{i} \times \pmb{o}) + (\pmb{o}) \end{align}$$

RNN

Given

• $\pmb{n}$ # of FFNN in each unit
  • RNN: 1
  • GRU: 3
  • LSTM: 4
• $\pmb{i}$ input size
• $\pmb{h}$ hidden size

For each FFNN, the input state and previous hidden state are concatenated, thus each FFFN has $\pmb{(h+i) \times h} + \pmb{h}$ parameters.

The total # of params is

$$\pmb{n} \times \left[ \pmb{(h+i) \times h} + \pmb{h} \right]$$

• LSTM: $4 \times \left[ \pmb{(h+i) \times h} + \pmb{h} \right]$
• GRU: $3 \times \left[ \pmb{(h+i) \times h} + \pmb{h} \right]$
• RNN: $1 \times \left[ \pmb{(h+i) \times h} + \pmb{h} \right]$

LSTMs

$$\left[\begin{array}{c} \mathbf{i}^c_j\\ \mathbf{o}^c_j \\ \mathbf{f}^c_j \\ \tilde{c}^c_j \end{array}\right] = \left[\begin{array}{c} \sigma \\ \sigma \\ \sigma \\ \tanh \end{array}\right] (\mathbf{W}^{c^T} \left[\begin{array}{c} \mathbf{x}^c_j \\ \mathbf{h}^c_{j-1}\end{array}\right] + \mathbf{b}^c)$$

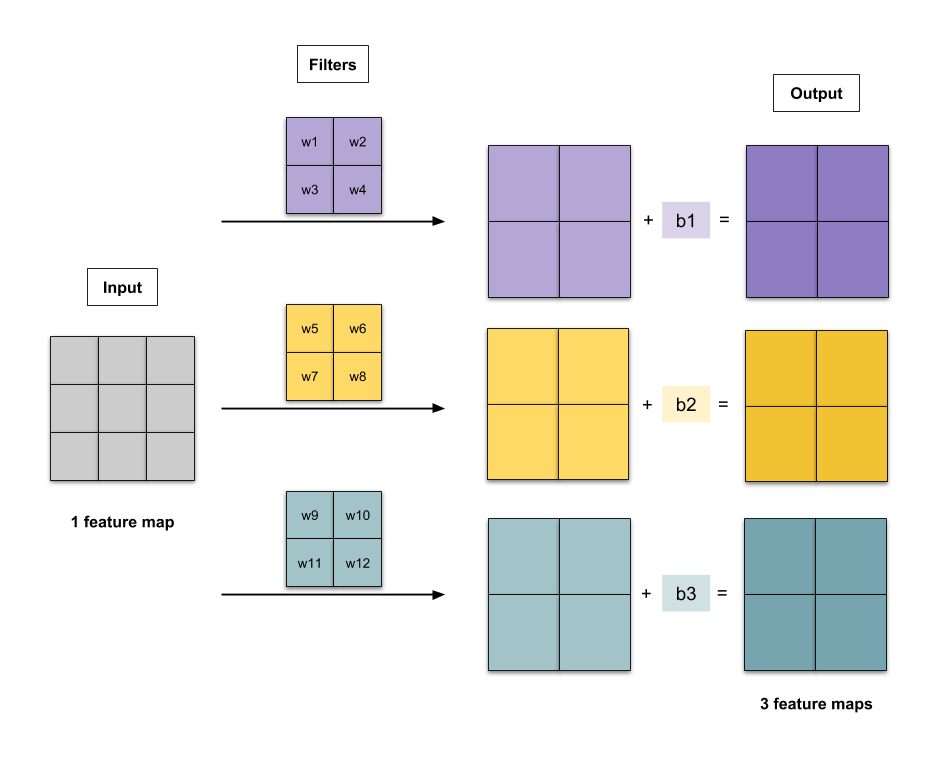
CNN

Given

• $\pmb{i}$ input channel
• $\pmb{f}$ filter size
• $\pmb{o}$ output channel (i.e. # of filters)

$$\# \text{ of params} = [\pmb{i} \times (\pmb{f} \times \pmb{f}) \times \pmb{o}] + \pmb{o}$$

Image source: ^[2]

Transformers

Given

• $\pmb{x}$ denotes the embedding dim == model dimension == output dimension

MHDPA

• Scaled dot product $$\text{Attention}(\mathbf{Q}W_Q^\top, \mathbf{K}W_K^\top, \mathbf{V}W_V^\top) = \text{softmax}(\frac{(\mathbf{Q}W_Q^\top) (\mathbf{K}W_K^\top)^\top}{\sqrt{d_{k}}})(\mathbf{V}W_V^\top)$$

• Multi-head dot product attention (MHDPA)

  $$\text{MultiHead}(\mathbf{Q},\mathbf{K},\mathbf{V}) = \text{concat}(\text{head}_1,...,\text{head}_h) \mathbf{W}^O$$

• Overall, MHDPA has 4 linear connections (i.e., K, V, Q, output after concat). There are $4 \times \left[ (\pmb{x} \times \pmb{x}) + \pmb{x} \right]$ trainable parameters.

Transformer Encoder

Given

• $\pmb{m}$ is # of encoder stacks

• Layer normalization

  $$y = \gamma * \frac{x - E[x]}{\sqrt{\text{Var}[x]+\epsilon}} + \beta$$

  the param number of single layer norm is sum the count of weights $\gamma$ and biases $\beta$: $\pmb{x}+\pmb{x}$

• FFNN: param number of two linear layers = $(\pmb{x} \times \pmb{4x} + \pmb{4x}) + (\pmb{4x} \times \pmb{x} + \pmb{x})$

Thus the total number of transformer encoder is: sum the number of 1 MHDPA, 2 Layer norm, 1 two-layer FFNN, times the stack number $\pmb{m}$:

$$\pmb{m} \times [1 \times \underbrace{\big(4 \times \left[ (\pmb{x} \times \pmb{x}) + \pmb{x} \right]\big)}_\text{MHDPA} + 2 \times \underbrace{\big( \pmb{x}+\pmb{x} \big)}_\text{Layer Norm} + \underbrace{\big( 2\times 4\pmb{x} \times \pmb{x} + 5\pmb{x} \big)}_\text{FFNN}]$$

Transformer Decoder

Given

• $\pmb{n}$ is # of decoder stacks

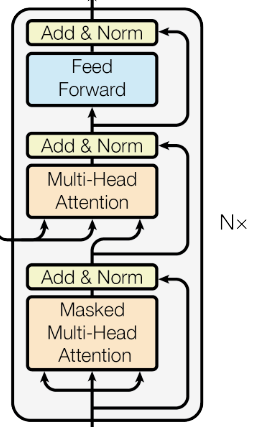
The total number of transformer decoder is: sum the number of 2 MHDPA, 3 Layer norm, 1 two-layer FFNN, times the stack number $\pmb{n}$:

$$\pmb{n} \times [2 \times \underbrace{\big(4 \times \left[ (\pmb{x} \times \pmb{x}) + \pmb{x} \right]\big)}_\text{MHDPA} + 3 \times \underbrace{\big( \pmb{x}+\pmb{x} \big)}_\text{Layer Norm} + \underbrace{\big( 2\times 4\pmb{x} \times \pmb{x} + 5\pmb{x} \big)}_\text{FFNN}]$$

References

---

1. 1.Towards data science: Counting No. of Parameters in Deep Learning Models by Hand ↩
2. 2.Towards data science: Animated RNN, LSTM and GRU ↩
3. 3.Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones, L., Gomez, A. N., ... & Polosukhin, I. (2017). Attention is all you need. In Advances in neural information processing systems (pp. 5998-6008). ↩