Dynamic Programming (DP) is ubiquitous in NLP, such as Minimum Edit Distance, Viterbi Decoding, forward/backward algorithm, CKY algorithm, etc.

Minimum Edit Distance

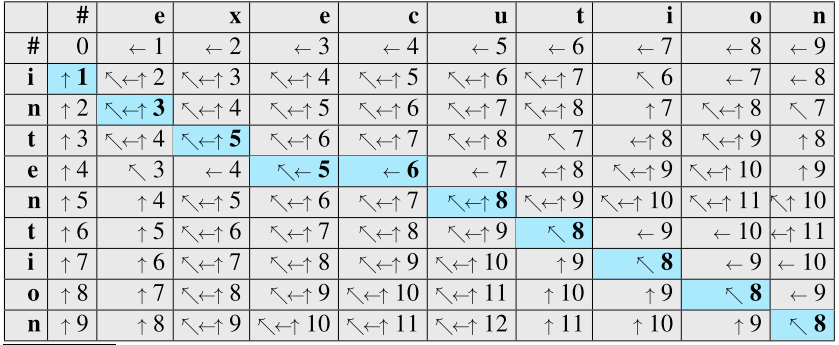
Minimum Edit Distance (Levenshtein distance) is string metric for measuring the difference between two sequences.

Given two strings $a$ and $b$ (with length $|a|$ and $|b|$ respectively), define $\text{D}(i,j)$ as the edit distance between $a[1 \cdots i]$ and $b[1 \cdots j]$, i.e. the first $i$ chars of $a$ and the first $j$ chars of $b$. The edit distance between two strings is $\text{D}(|a|, |b|)$.

$\text{D}[i,j]=\left\{ \begin{array}{ll} D[i-1, j] + \text{del-cost}(a[i])\\ D[i, j-1] + \text{ins-cost}(b[j])\\ D[i-1, j-1] + \text{sub-cost}(a[i], b[j]) \end{array} \right.$

Let the costs of insertion, deletion, substitution are 1,1 and 2, respectively.

$\text{D}[i,j]=\min\left\{ \begin{array}{ll} D[i-1, j] + 1\\ D[i, j-1] + 1\\ D[i-1, j-1] + \left\{ \begin{array}{ll} 2 \quad \text{if a[i] }\neq{ b[j]}\\ 0 \quad \text{if a[i] == b[j]} \end{array} \right. \end{array} \right.$

That is,

$\text{D}[i,j]=\left\{ \begin{array}{ll} D[i-1, j-1] & \quad \text{if a[i] == b[j]} \\ \min(D[i-1, j]+1, D[i, j-1]+1, D[i-1, j-1]+2) & \quad \text{if a[i] }\neq\text{ b[j]} \end{array} \right.$

Algorithms in Python:

class Solution:
    def minDistance(self, word1, word2):
        """
        Levenshtein distance
        :type word1: str
        :type word2: str
        :rtype: int
        """
        m, n = len(word1) + 1, len(word2) + 1
        dp = [[0 for _ in range(n)] for _ in range(m)]
        for i in range(m):
            dp[i][0] = i
        for j in range(n):
            dp[0][j] = j
        for i in range(1, m):
            for j in range(1, n):
            	# implementation 1
                # --------------------------
            	# if word1[i - 1] == word2[j - 1]:
                #     sub_cost = 0
                # else:
                #     sub_cost = 2
                # dp[i][j] = min(dp[i - 1][j] + 1, dp[i][j - 1] + 1, dp[i - 1][j - 1] + sub_cost)
                # implementation 2
                # ===========================
                if word1[i - 1] == word2[j - 1]:
                    dp[i][j] = dp[i - 1][j - 1]
                else:
                    dp[i][j] = min(dp[i - 1][j] + 1, dp[i][j - 1] + 1, dp[i - 1][j - 1] + 2)
        return dp[m - 1][n - 1]

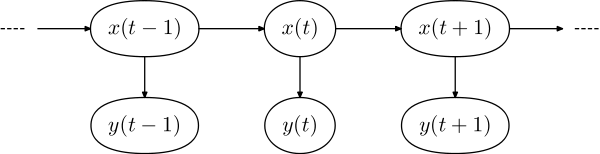
DP in HMMs

Hidden Markov Models (HMMs) describe the joint probability of its hidden(unobserved) and observed discrete random variables. It relies on the Markov assumption and output indenpendence.

The observation sequence $Y = (Y_1=y_1, Y_2=y_2, \cdots, Y_T=y_T)$
Let $X_t$ be a discrete random vriable with $K$ possible states. The transition matrix $A={a_{ij}} = P(X_t=j \vert X_{t-1}=i)$
The initial state distribution(t=1) is $\pi_i = P(X_1 = i)$
The output/emission matrix $B = {b_j(y_i)} = P(Y_t=y_i \vert X_t = j)$

Thus the hidden markov chain can be defined by $\theta = (A, B, \pi)$ .

Forward algorithm

Forward algorithm is used to calculate the "belief state": the probability at time $t$, given the history of evidence.^[1] Such process is also called filtering.

The goal is to compute the joint probability $p(x_t, y_{1:t})$ , which requires marginalizing over all possible state sequence ${x_{1:t-1}}$ , the # of which grows exponentially with $t$.
The conditional independence of HMM could help to perform calculation recursively.
Time complexity: $O(K^2T)$

$\begin{align} \pmb{\alpha_t(x_t)} &= p(x_t, y_{1:t}) & \\ & = \sum_{x_{t-1}} p(x_t, x_{t-1}, y_{1:t}) & \\ & = \sum_{x_{t-1}} p(y_t \vert x_t, x_{t-1}, y_{1:t-1}) p(x_{t} \vert x_{t-1}, y_{1:t-1}) p(x_{t-1, y_{1:t-1}}) & \text{chain rule} \\ & = \underbrace{p(y_t \vert x_t)}_\text{emission prob.} \sum_{x_{t-1}} \underbrace{ p(x_t \vert x_{t-1})}_\text{transition prob.} \pmb{\alpha_{t-1}(x_{t-1})} & \text{Markov assumption} \\ \end{align}$

Forward algorithm:

Init $t=0$, transition probabilities $p(x_t \vert x_{t-1})$ , emission probabilities $p(y_j \vert x_i)$ , observed sequence $y_{1:t}$
for $t \leftarrow t+1, \cdots, T$: $\pmb{\alpha_t(x_t)} \leftarrow p(y_t \vert x_t) \sum_{x_{t-1}} p(x_t \vert x_{t-1}) \pmb{\alpha_{t-1} (x_{t-1})}$ $p(y_{1:t}) = \alpha_T$ return $\alpha_T$

Viterbi Algorithm

Viterbi algorithm is to finding the most probable sequence of hidden states, i.e. Viterbi path.^[2]

Input:

The observation space $\pmb{O} = {o_1, o_2, \cdots, o_N }$
state space $S = {s_1, s_2, \cdots, s_K}$
initial probability array $\Pi = (\pi_1, \pi_2, \cdots, \pi_K)$ such that $\pi_i = p(x_1 = s_i)$
observation sequence $Y = {y_1, y_2, \cdots, y_T}$
transition matrix $A$ with size $K \times K$. $A_{ij}$ stores the transition probability of transition from state $s_i$ to $s_j$
emission matrix $B$ of size $K \times N$, such that $B_{ij}$ stores the probability of observing $o_j$ from state $s_i$

Output:

the most likely hidden state sequence $X = (x_1, x_2, \cdots, x_T)$
Time complexity: $O(|S|^2T)$

function Viterbi($O$,$S$, $\pi$, $Y$, $A$, $B$): returns $X$
1. for state i = do
  - Viterbi init step $0 \rightarrow 1$ : $T_1[i,1] \leftarrow \pi_i \cdot B_{iy_1}$
  - Backtrack init step $0 \rightarrow 1$ : $T_2[i,1] \leftarrow 0$
2. for observation $j = 2,3,\cdots, T$:
  - for state $i = 1,2,\cdots,K$:
    - Viterbi records the best prob $T_1[i,j] \leftarrow \max_k \big( T_1[k,j-1] \cdot A_{ki} \cdot B_{iy_j} \big)$
    - Backpointer saves the best backpointer $T_2[i,j] \leftarrow \arg\max_k \big( T_1[k,j-1] \cdot A_{ki} \big)$
3. best path prob. $Z_T \leftarrow \arg\max_k\big( T_1[k,T] \big)$
4. best path pointer $x_T \leftarrow s_{z_T}$
5. for $j=T, T-1, \cdots, 2$:
  1. do back tracking $z_{j-1} \leftarrow T_2[z_j,j]$
  2. Prev hidden state $x_{j-1} \leftarrow s_{z_{j-1}}$
6. return $X= (x_1, x_2, \cdots, x_T)$

Baum-Welch algorithm

Baum-Welch algorithm, as a speciqal case of EM algorithms, uses the forward-backward algorithm to find the maximum likelihood estimate of the unknown parameters of a HMM given a set of observed feature vectors.

The local maximum $\theta^* = \arg\max_\theta P(Y \vert \theta)$

Forward process

Let $\alpha_i(t) = P(Y_1=y_1, \cdots, Y_t=y_t, X_t=i \vert \theta)$ represent the probability of the observation of $y_1,y_2,\cdots,y_t$ :

$\begin{align} \alpha_i(1) &= \pi_i b_i (y_1) \\ \alpha_{i}(t+1) &= b_i(y_{t+1}) \sum_{j=1}^K \alpha_j(t)a_{ji} \end{align}$

backward process

Let $\beta_i(t)= P(Y_{t+1}=y_{t+1},\cdots,y_T=y_T \vert X_t=i,\theta)$ denote the probability of the sequence $y_{t+1}, \cdots, y_T$ starting at time $t$.

$\beta_i(t)=\left\{ \begin{array}{ll} \begin{align} \sum_{j=1}^K \beta_j(t+1) a_{ij}b_j(y_{t+1}) & \text{ if } t\neq T\\ 1 & \text{ if } t = T \end{align} \end{array} \right.$

update

The prob. of being state $i$ at time $t$ given the observation $Y$ and parameters $\theta$

$\gamma_i(t) = P(X_t=i \vert Y, \theta) = \frac{P(X_t=i, Y \vert \theta)}{P(Y \vert \theta)} = \frac{\alpha_i(t)\beta_i(t)}{\sum_{j=1}^K \alpha_j(t)\beta_j(t)}$

The prob. of being state $i$ and $j$ at times $t$ and $t+1$ respectively given the observation $Y$ and parameter $\theta$

$\begin{align} \xi_{ij}(t) &= P(X_t=i, X_{t+1}=j \vert Y, \theta) \\ & = \frac{P(X_t=i, X_{t+1}=j, Y \vert \theta)}{P(Y\vert \theta)} \\ & = \frac{\alpha_{i}(t) a_{ij} \beta_j(t+1) b_j(y_{t+1}) }{ \sum_{i=1}^K \sum_{j-1}^K \alpha_i(t) a_{ij} \beta_j(t+1)b_j(y_{t+1}) } \end{align}$

Update the HMM $\theta$:

$\pi$ at state $i$ at time 1: $\pi^*_i = \gamma_i(1)$
the transition matrix $A$. $\begin{align} a_{ij}^* &= \frac{\text{The expected # of transitions from state i to j}}{\text{the expected totoal # of transitions away from state i}}\\ & = \frac{\sum_{t=1}^{T-1}\xi_{ij}(t)}{\sum_{t=1}^{T-1}\gamma_i(t)} \end{align}$
the emission matrix $B$
- where $\mathcal{1}_{y_t=v_k} = \left\{ \begin{array}{ll} 1 \quad \text{ if } y_t=v_k\\ 0 \quad \text{ otherwise} \end{array} \right.$

CKY algorithm

TBD

Yekun's Note

Dynamic Programming in NLP