Activation functions lead to non-linearity in neural networks. Most common types are Sigmoid, Tanh, Relu, etc.

Commonly-used Activations

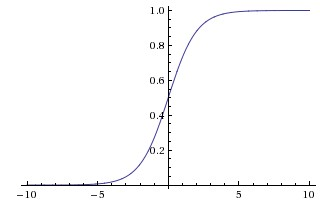
Sigmoid

$\sigma(x) = \frac{1}{1+e^{-x}}$

Sigmoid function takes a real-valued number and ‘squashes’ it into the range (0,1).

Drawbacks:

Sigmoids saturate and kill gradients. When at either the tail of 0 or 1, the gradient is almost zero. Take care of the weight initialization: if too large most neurons would saturate soon and the networks will barely learn.
Outputs are not zero-centered.

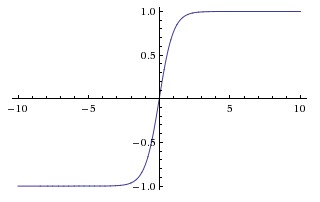
Tanh

$\tanh(x) = \frac{e^x-e^{-x}}{e^x+e^{-x}} = 2\sigma(2x) -1$

Tanh squashes the real number input into the range [-1,1].

Like sigmoid, its activations saturate;
but the output of tanh is zero-centered. Therefore, tanh non-linearity is always preferred to the sigmoid non-linearity.
$\tanh$ is simply a scaled sigmoid neuron: $\tanh(x) = 2 \sigma(2x) -1$

ReLU (Rectified Linear Unit)

$\text{Relu}(x) = \max(0, x)$

ReLu is simply thresholded at zero.

Pros:

6x accecerate the convergence of SGD compared to the tanh functions.^[2]
No expensive operations (e.g. exponential)
Problems:
Fragile during training and can “die”: ReLU units can irreversibly die during training.

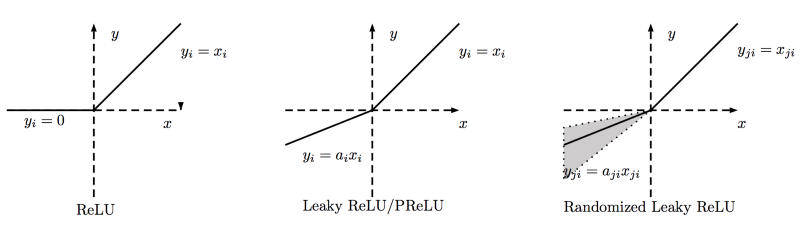
Leaky ReLU

$f(x)=\left\{ \begin{array}{ll} \begin{align} x \quad & x>=0\\ \alpha x \quad & x<0\\ \end{align} \end{array} \right.$

Leaky ReLU attempts to fix the dying ReLU problem, by setting a small nagative slope when $x<0$. However, the consistency of the benefits across tasks is unclear.

PReLU

Parametric ReLU

$f(x) = \max(\alpha x, x)$

where $\alpha$ is learnable.

ELU (Exponential Linear Units)

ELU ^[4]

$f(x)=\left\{ \begin{array}{ll} \begin{align} x \quad & x>=0\\ \alpha (\exp(x)-1) \quad & x<0\\ \end{align} \end{array} \right.$

Maxout

See Maxout Networks(Goodfellow et.al 2013)^[3] :

$f(x) = \max(w_1^Tx+b_1, w_2^Tx + b_2)$

GELU (Gaussian Error Linear Units)

Motivation:

combine the properties of dropout, zoneout, and ReLUs.^[5]
multiplying the input by zero or one, but the values of this zero-one mask are stochastically determined while also dependent upon the input.

Specically, multiply the neuron input $x$ by $m \sim \text{Benoulli}(\Phi(x))$, where $\Phi(x)=P(X \leq x)$, $X \sim \mathcal{N}(0,1)$.

The non-linearity is the expected transformation of the stochastic regularizer on an input $x$:
$\Phi(x) \times I x + (1-\Phi(x)) \times 0x = x \Phi(x)$

Then define the Gaussian Error Linear Unit (GELU) as:

$\begin{align} \text{GELU}(x) &= x P(X \leq x) = x \Phi(x) \\ & \approx 0.5x (1+ \tanh [\sqrt{\frac{2}{\pi}} (x+ 0.044715x^3)]) \\ &= x \sigma(1.702x) \end{align}$

BERT implementation:

def gelu(x):
  """Gaussian Error Linear Unit.
  This is a smoother version of the RELU.
  Original paper: https://arxiv.org/abs/1606.08415
  Args:
    x: float Tensor to perform activation.
  Returns:
    `x` with the GELU activation applied.
  """
  cdf = 0.5 * (1.0 + tf.tanh(
      (np.sqrt(2 / np.pi) * (x + 0.044715 * tf.pow(x, 3)))))
  return x * cdf

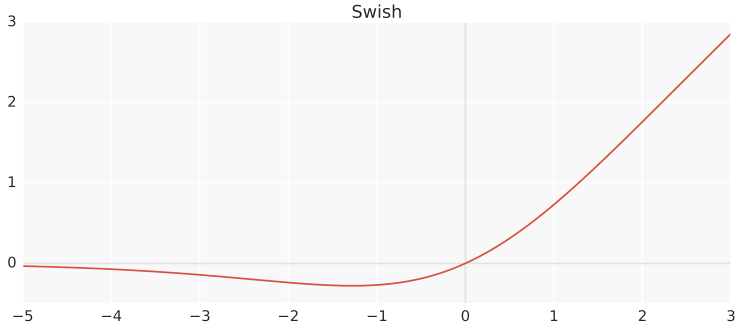
Swish

Swish has the property of one-sided boundaries at zero, smoothness and non-monotonicity. Swish is shown to outperform ReLU on many tasks.^[6]

$f(x) = x \cdot \sigma (x)$

Personally, this idea is borrowed from the work of (Dauphin et. al, 2017)^[7] at FAIR in 2017, Gated Linear Unit(GLU) in gated CNNs, which is used to capture the sequential information after temporal convolutions:

$H_l(\pmb{X}) = (\pmb{X} * \pmb{W} + \pmb{b}) \otimes \sigma ((\pmb{X} * \pmb{V} + \pmb{b}))$

Relu can be seen as a simplication of GLU, where the activation of the gate depends on the sign of the input:

$\text{Relu}(\pmb{X}) = \pmb{X} \otimes (\pmb{X} > 0)$

The gradient of LSTM-style gating of Gated Tanh Unit (GTU) is gradually vanishing because of the downscaling factors $\color{salmon}{\tanh’(\pmb{X})}$ and $\color{salmon}{\sigma’(\pmb{X})}$:

$\nabla [ \tanh (\pmb{X}) \otimes \sigma(\pmb{X})] = \color{salmon}{\tanh'(\pmb{X})} \nabla \pmb{X} \otimes \sigma (\pmb{X}) + \color{salmon}{\sigma'(\pmb{X})} \nabla \pmb{X} \otimes \tanh(\pmb{X})$

GLU has the path $\color{green}{\nabla \pmb{X} \otimes \sigma(\pmb{X})}$, which does not downscale the activated gating unit. This can be thought as a multiplicative skip connection.

$\nabla[\pmb{X} \otimes \sigma(\pmb{X})] = \color{green}{\nabla \pmb{X} \otimes \sigma(\pmb{X})} + \pmb{X} \otimes \sigma'(\pmb{X}) \nabla \pmb{X}$

import torch.nn.functional as F

def Swish(x):
	return x*F.sigmoid(x)

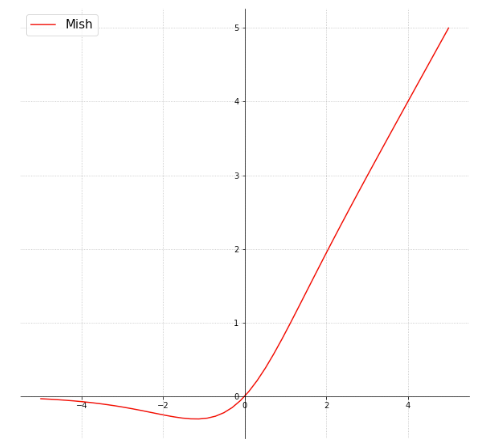
Mish

Mish is a non-monotonic, self-gated/regularized, smoothing activation function. It is shown to outperform Swish and ReLU on various tasks.^[8]

$f(x) = x \cdot \tanh \big( \underbrace{\ln (1+ \exp(x))}_\text{Softplus} \big)$

References

1.http://cs231n.github.io/neural-networks-1/ ↩
2.Nair, V., & Hinton, G. E. (2010). Rectified linear units improve restricted boltzmann machines. In Proceedings of the 27th international conference on machine learning (ICML-10) (pp. 807-814). ↩
3.Goodfellow, I. J., Warde-Farley, D., Mirza, M., Courville, A., & Bengio, Y. (2013). Maxout networks. arXiv preprint arXiv:1302.4389. ↩
4.Clevert, D. A., Unterthiner, T., & Hochreiter, S. (2015). Fast and accurate deep network learning by exponential linear units (ELUs). arXiv preprint arXiv:1511.07289. ↩
5.Hendrycks, D., & Gimpel, K. (2016). Gaussian Error Linear Units (GELUs). arXiv preprint arXiv:1606.08415. ↩
6.Ramachandran, P., Zoph, B., & Le, Q. V. (2017). Swish: a self-gated activation function. arXiv preprint arXiv:1710.05941. ↩
7.Dauphin, Y. N., Fan, A., Auli, M., & Grangier, D. (2017, August). Language modeling with gated convolutional networks. In Proceedings of the 34th International Conference on Machine Learning-Volume 70 (pp. 933-941). JMLR. org. ↩
8.Misra, D. (2019). Mish: A Self Regularized Non-Monotonic Neural Activation Function. arXiv preprint arXiv:1908.08681. ↩

Yekun's Note

An Introduction to Activation Functions