Planning by Dynamic Programming (RL)

Notes of lectures by D. Silver.

Introduction

• Dynamic: sequential or temporal components to the problem

• Programming: optimizing a “program”, i.e. a policy
  c.f. linear programming

• Breaking down the complex problems into subproblems

  • Solve the problems
  • Combine solutions to subproblems

Requirements for dynamic programming

Dynamic programming(DP) is general solution for problems with two properties:

• Optimal substructure
  • Principle of optimality applies
  • Optimal solution can be decomposed into subproblems
• Overlapping subproblems
  • Subproblems recur many times
  • Solutions can be cached and reused

MDP satisfy both properties:

• Bellman equation gives recursive decomposition
• Value function stores and reuses solutions

Planning by DP

• DP assumes full knowledge of the MDP
• It is used for planning in an MDP
• For prediction:
  1. Input: DMP $<\mathcal{S}, \mathcal{A},\mathcal{P},\mathcal{R},\mathcal{\gamma}>$ and policy $\pi$, or MRP $<\mathcal{S},\mathcal{P}^{\pi},\mathcal{R}^{\pi},\mathcal{\gamma}>$
  2. Output: value function $v_{\pi}$
• For control:
  1. Input: MDP $<\mathcal{S}, \mathcal{A},\mathcal{P},\mathcal{R},\mathcal{\gamma}>$
  2. Output: optimal value function $v_{*}$, and optimal policy $\pi_{*}$

Other applications by DP

• Scheduling algorithms
• String algorithms (e.g. sequence alignment)
• Graph algorithms (e.g. shortest path algorithms)
• Graphical models (e.g. Viterbi algorithm)
• Bioinformatics (e.g. lattice model)

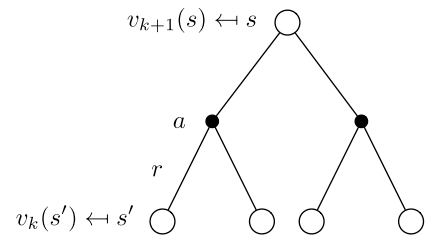
Iterative policy evaluation

• Problem: evaluate a given policy $\pi$
• Solution: iterative application of Bellman expectation backup

$$v_1 \rightarrow v_2 \rightarrow ... \rightarrow v_{\pi}$$

Using synchronous backups:

• At each iteration $k+1$
• For all states $s \in \mathcal{S}$
• Update $v_{k+1}(s)$ from $v_{k}(s')$, where $s’$ is a successor state of $s$

$$v_{k+1}(s) = sum_{a \in \mathcal{A}} \pi(a \vert s) \Big( \mathcal{R}_s^a + \gamma \sum_{s' \in \mathcal{S}} \mathcal{P}_{ss'}^{a} v_k(s') \Big)$$ $$\pmb{v}^{k+1} = \pmb{\mathcal{R}^{\pi}} + \gamma \pmb{\mathcal{P}^{\pi}v}^k$$

Policy iteration

How to improve a policy

Given a policy $\pi$:

• Evaluate the policy $\pi$ $$v_{\pi}(s) = \mathbb{E}[R_{t+1} + \gamma R_{t+2} + ... | S_t = s]$$
• Improve the policy by acting greedily w.r.t $v_{\pi}$ $$\pi' = \text{greedy}(v_{\pi})$$

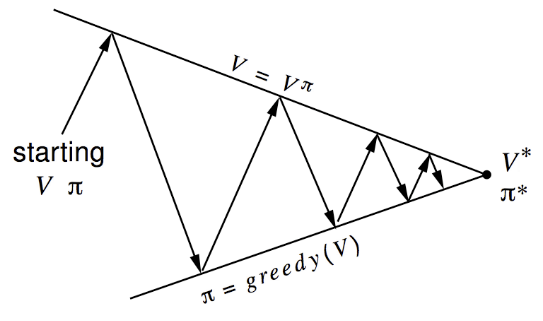
• Policy evaluation: estimate $v_{\pi}$ (iterative policy evaluation)

• Policy improvement: generate $\pi' \leq \pi$ (greedy policy improvement)

Policy improvement

Consider a deterministic policy $a=\pi(s)$

• Improve the policy by acting greedily $$\pi'(s) = \arg\max_{a \in \mathcal{A}} q_{\pi}(s,a)$$

This improves the value from any state $s$ over one step

$$q_{\pi}(s, \pi'(s)) = \max_{a \in \mathcal{A}}q_{\pi}(s,a) \leq q_{\pi}(s, \pi(s)) = v_{\pi}(s)$$

It therefore improves the value function $v_{\pi'}(s) \leq v_{\pi}(s)$

$$v_{\pi}(s) \leq q_{\pi}(s, \pi'(s)) = \mathbb{E}_{\pi'}[R_{t+1} + \gamma v_{\pi}(S_{t+1})|S_t = t ] \\ \leq \mathbb{E}_{\pi'}[R_{t+1} + \gamma q_{\pi}(S_{t+1}, \pi'(S_{t+1}))|S_t=s] \\ \leq \mathbb{E}_{\pi'}[R_{t+1}+\gamma R_{t=2}+ \gamma^2 q_{\pi} (S_{t+2}, \pi'(S_{t+2}))|S_t = s] \\ \leq \mathbb{E}_{\pi'}[R_{t+1}+ \gamma R_{t+2}+... | S_t=s] = v_{\pi'}(s)$$

• If improvements stop, $$q_{\pi} (s, \pi'(s)) = \max_{a \in \mathcal{A}} q_{\pi}(s, a) = q_{\pi}(s, \pi(s)) = v_{\pi}(s)$$

• Then the Bellman optimality equation has been satisfied

  $$v_{\pi}(s) = \max_{a \in \mathcal{A}} q_{\pi}(s,a)$$

• Therefore $v_{\pi}(s) = v_{*}(s)$ for all $s \in \mathcal{S}$. So $\pi$ is an optimal policy

Value iteration

Value iteration in MDPs

Principle of Optimality

An optimal policy can be subdivided into two components:

• An optimal first action $A_{*}$
• Followed by an optimal policy from successor state $S’$

Deterministic value iteration

If we know the solution to subproblems $v_{*}(s')$, then solution $v_{*}(s)$ can be found by one-step lookahead:

$$v_{*}(s) \leftarrow \max_{a \in \mathcal{A}} \mathcal{R}_s^a + \gamma \sum_{s' \in \mathcal{S}} \mathcal{P}_{ss'}^{a} v_{*}(s')$$

• The idea of value iteration is to apply these update iteratively
• Intuition: start with final rewards and work backwards
• Still works loopy, stochastic MDPs

Value iteration

• Problems: find optimal policy $\pi$

• Solution: iterative application of Bellman optimality backup

  $$v_1 \rightarrow v_2 \rightarrow ... \rightarrow v_{*}$$

• Using synchronous backups at each iteration $k+1$, for all states $s \in \mathcal{S}$, update $v_{k+1}(s)$ from $v_{k}(s')$

• Unlike policy iteration , there is no explicit policy

$$v_{k+1}(s) = \max_{a \in \mathcal{A}} \big( \mathcal{R}_s^a + \gamma \sum_{s' \in \mathcal{S}} \mathcal{P}_{ss'}^a v_{k}(s') big)$$ $$\pmb{v}_{k+1} = \max_{a \in \mathcal{A}} \pmb{R^a} + \gamma \pmb{\mathcal{P}^a v}_k$$

Synchronous DP algorithms

Problem	Bellman equation	Algorithm
Prediction	Bellman Expectation Equation	Iterative Policy Evaluation
Control	Bellman Expectation Equation + Greedy Policy Improvement	Policy Iteration
Control	Bellman Optimality Equation	Value Iteration

Asynchronous DP

In-place DP

• Synchronous value iteration stores two copies of value function for all $s$ in $\mathcal{S}$:

  $$\pmb{v_{new}(s)} \leftarrow \max{a \in \mathcal{A}} \big( \mathcal{R}_s^a + \gamma \sum{s' \in \mathcal{S}} P_{ss'}^a \pmb{v_{old}(s')} \big)$$ $$\pmb{v_{old}} \leftarrow \pmb{v_{new}}$$

• In-place value iteration only stores one copy of value function for all $s$ in $\mathcal{S}$:

  $$\pmb{v(s)} \leftarrow \max{a \in \mathcal{A}} \big( \mathcal{R}_s^a + \gamma \sum{s' \in \mathcal{S}} P_{ss'}^a \pmb{v(s')} \big)$$

Prioritized sweeping

Use magnitude of Bellman error to select state

$$\big| \max_{a \in \mathcal{A}} \big( \mathcal{R}_s^a + \gamma \sum_{s' \in \mathcal{S}} \mathcal{P}_{ss'}^a v(s') \big) - v(s) \big|$$

Backup the state with the largest remaining Bellman error

Real-time DP

• Idea: only states that are relevant to agent
• Use agent’s experience to guide the selection of states
• After each time-step $S_t, A_t, R_{t+1}$
• Backup the state $S_t$

$$\pmb{v(S_t)} \leftarrow \max_{a \in \mathcal{A}} \big( \mathcal{R}_{\pmb{S_t}}^a + \gamma \sum_{s' \in \mathcal{S}} \mathcal{P}_{\pmb{S_t}s'}^a \pmb{v(s')} \big)$$